题目内容
设抛物线y=ax2+bx+c(a≠0)过A(0,1),B(2,3),C三点,其中点C在直线x=
上,且点C到抛物线的对称轴的距离等于
,则抛物线的解析式为 .
| 1 |
| 2 |
| 3 |
| 2 |
考点:待定系数法求二次函数解析式
专题:计算题
分析:根据点C在直线x=
上,且点C到抛物线的对称轴的距离等于
,确定出抛物线对称轴,利用对称轴公式列出方程,再将A与B代入抛物线解析式得到关于a与b的方程,联立求出a与b的值,即可确定出解析式.
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:由题意得到抛物线对称轴为x=-1或x=2,
当对称轴为直线x=-1时,则有-
=-1,即b=2a①,
将A与B坐标代入抛物线解析式得:
,
消去c得:2a+b=1②,
①代入②,解得:a=
,b=
,
此时抛物线解析式为y=
x2+
x+1;
当对称轴为直线x=2时,则有-
=2,即b=-4a,
与2a+b=1联立,解得:a=-
,b=2,
此时抛物线解析式为y=-
x2+2x+1.
故答案为:y=
x2+
x+1或y=-
x2+2x+1
当对称轴为直线x=-1时,则有-
| b |
| 2a |
将A与B坐标代入抛物线解析式得:
|
消去c得:2a+b=1②,
①代入②,解得:a=
| 1 |
| 4 |
| 1 |
| 2 |
此时抛物线解析式为y=
| 1 |
| 4 |
| 1 |
| 2 |
当对称轴为直线x=2时,则有-
| b |
| 2a |
与2a+b=1联立,解得:a=-
| 1 |
| 2 |
此时抛物线解析式为y=-
| 1 |
| 2 |
故答案为:y=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在以下四个图案中,是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
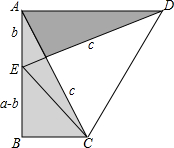 如图,两个全等的直角△ABC和△DAE,两直角边的长分别为a,b,斜边长为c,使用两种不同的方法表示梯形ABCD的面积,并以此来验证勾股定理.
如图,两个全等的直角△ABC和△DAE,两直角边的长分别为a,b,斜边长为c,使用两种不同的方法表示梯形ABCD的面积,并以此来验证勾股定理. 如图所示,一般书本的纸张是原纸张多次对开得到矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,若各种开本的矩形都相似,那么
如图所示,一般书本的纸张是原纸张多次对开得到矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,若各种开本的矩形都相似,那么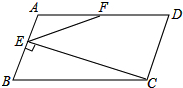 如图,?ABCD中,BC=2CD,CE⊥AB于点E,F为AD的中点,若∠EFD=k∠AEF,求k的值.
如图,?ABCD中,BC=2CD,CE⊥AB于点E,F为AD的中点,若∠EFD=k∠AEF,求k的值.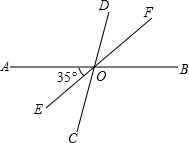 直线AB,CD相交于O,过点O画射线OE,OF,已知∠AOE=35°,∠EOC=∠DOF
直线AB,CD相交于O,过点O画射线OE,OF,已知∠AOE=35°,∠EOC=∠DOF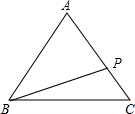 在三角形ABC中,AB=AC=5,BC=6,点P为AC上的一个动点,PB的取值范围是
在三角形ABC中,AB=AC=5,BC=6,点P为AC上的一个动点,PB的取值范围是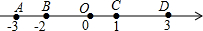 定义:若数轴上A、B两点分别对应数a、b,则A、B两点之间的距离记作|AB|,|AB|=|a-b|,根据图中信息,完成下列各题:
定义:若数轴上A、B两点分别对应数a、b,则A、B两点之间的距离记作|AB|,|AB|=|a-b|,根据图中信息,完成下列各题: