题目内容
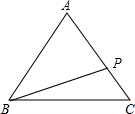在三角形ABC中，AB=AC=5，BC=6，点P为AC上的一个动点，PB的取值范围是考点：勾股定理,垂线段最短,等腰三角形的性质
专题：
分析：作BF⊥AC，垂足为F．利用勾股定理列出式子AB2-AF2=BF2=BC2-CF2，设AF=x，则CF=5-x，代入后求出x的值，从而求出BF的长，即为BP的最小值，BC的长即为BP的最大值．
解答：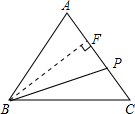
解：作BF⊥AC，垂足为F．
由勾股定理可得AB2-AF2=BF2=BC2-CF2，
设AF=x，则CF=5-x，
则有52-x2=62-（5-x）2，
解得x=
，
BF=
=
，
可得PB的取值范围是
≤PB≤6．
故答案为
≤PB≤6．
解：作BF⊥AC，垂足为F．由勾股定理可得AB2-AF2=BF2=BC2-CF2，
设AF=x，则CF=5-x，
则有52-x2=62-（5-x）2，
解得x=
| 7 |
| 5 |
BF=
52-(
|
| 24 |
| 5 |
可得PB的取值范围是
| 24 |
| 5 |
故答案为
| 24 |
| 5 |
点评：本题考查了勾股定理、垂线段最短、等腰三角形的性质，正确作出辅助线是解题的关键．
练习册系列答案
相关题目
如图，CD平分∠BCA，∠1=∠2=30°，你知道∠DEA的度数吗？
如图，已知：AF、BD、CE、ABC、DEF均是直线，∠EQF=∠APB，∠C=∠D．根据如图所示的程序，若输入的自变量x的值为-1，则输出的因变量y的值为（ ）
| A、1 | ||
| B、-2 | ||
C、
| ||
| D、3 |
如图，四边形ABCD是圆内接四边形，E是AD延长线上一点，若∠CBA=120°，则∠EDC的大小是（ ）| A、60° | B、120° |
| C、150° | D、130° |
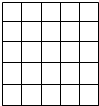如图：正方形网格中的每个小正方形边长都是1，任意连接这些小正方形的顶点，可得到一些线段．