Question

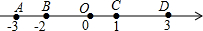定义：若数轴上A、B两点分别对应数a、b，则A、B两点之间的距离记作|AB|，|AB|=|a-b|，根据图中信息，完成下列各题：
（1）|AB|=

 

；
（2）若数轴上点P对应数x，则：
①当|PA|=2时，x=

 

；
②当|PB|+|PC|取最小值时，x的取值范围为

 

；
（3）求A、B、O、C、D这5个点中所有两点间的距离之和．

Answer 1

考点：绝对值,数轴,两点间的距离

专题：

分析：（1）根据题目已知中的A、B两点间的距离表示为|AB|=|a-b|．即可解答；
（2）使①中的式子等于2，解出即可；求|PB|+|PC|的最小值，由线段的性质，两点之间，线段最短，可知当-2≤x≤1时，|PB|+|PC|有最小值，再根据绝对值的性质即可求出最小值及x的取值
（3）根据两点间的距离公式，可得答案．

解答：解：（1）A、B两点间的距离表示为|AB|=|a-b|=|-3-（-2）|=1．
（2）①当|PA|=2时，即|x-（-3）|=2，解得：x=-1或-5；
②当|PB|+|PC|取最小值时，即可得|x-（-2）|+|x-1|取最小值时，|x-1|+|x+2|的最小值为3，此时x的取值是-2≤x≤1；
（3）A、B、O、C、D这5个点中所有两点间的距离之和=|AB|+|AO|+|AC|+|AD|+|BO|+|BC|+|BD|+|OC|+|OD|+|CD|=1+3+4+6+2+3+5+1+3+2=30
故答案为：（1）1；（2）①=-1或-5；②-2≤x≤1；（3）30

点评：考查了绝对值和数轴，借助数轴可以使有关绝对值的问题转化为数轴上有关距离的问题，反之，有关数轴上的距离问题也可以转化为绝对值问题．这种相互转化在解决某些问题时可以带来方便．事实上，|A-B|表示的几何意义就是在数轴上表示数A与数B的点之间的距离．