题目内容
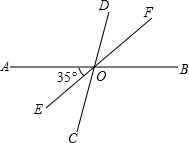 直线AB,CD相交于O,过点O画射线OE,OF,已知∠AOE=35°,∠EOC=∠DOF
直线AB,CD相交于O,过点O画射线OE,OF,已知∠AOE=35°,∠EOC=∠DOF(1)求∠AOF的度数;
(2)点E,O,F在同一条直线上吗?(要证明过程)
考点:对顶角、邻补角
专题:
分析:(1)根据邻补角定义先求出∠BOE,再根据对顶角相等,即可求出∠AOF的度数;
(2)证明∠AOF+∠AOE=180°即可证出结论.
(2)证明∠AOF+∠AOE=180°即可证出结论.
解答:(1)解:∵直线AB,CD相交于O,∠AOE=35°,
∴∠BOE=180°-∠AOE=145°,∠BOC=∠AOD,
即∠BOC+∠EOC=145°,
∵∠EOC=∠DOF,
∴∠AOF=∠AOD+∠DOF=∠BOC+∠EOC=145°;
(2)E,O,F在同一条直线上;
证明:∵∠AOF+∠AOE=145°+35°=180°,
∴E,O,F在同一条直线上.
∴∠BOE=180°-∠AOE=145°,∠BOC=∠AOD,
即∠BOC+∠EOC=145°,
∵∠EOC=∠DOF,
∴∠AOF=∠AOD+∠DOF=∠BOC+∠EOC=145°;
(2)E,O,F在同一条直线上;
证明:∵∠AOF+∠AOE=145°+35°=180°,
∴E,O,F在同一条直线上.
点评:本题考查了对顶角、邻补角的定义;弄清各个角之间的数量关系是解决问题的关键;注意(2)的证明方法.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
函数y=-
的自变量x的取值范围是( )
| ||
| x-1 |
| A、x<1 | B、x≥1 |
| C、x>1 | D、x≤1 |
下列说法中正确的是( )
| A、所有的矩形都相似 |
| B、所有的正方形都相似 |
| C、所有的菱形都相似 |
| D、所有的平行四边形都相似 |
 如图,四边形ABCD是圆内接四边形,E是AD延长线上一点,若∠CBA=120°,则∠EDC的大小是( )
如图,四边形ABCD是圆内接四边形,E是AD延长线上一点,若∠CBA=120°,则∠EDC的大小是( )| A、60° | B、120° |
| C、150° | D、130° |
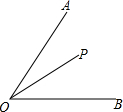 如图,∠AOB=45°,角内一点P,PO=10,两边上各有点Q,R(均不同于O),则△PQR的周长的最小值为
如图,∠AOB=45°,角内一点P,PO=10,两边上各有点Q,R(均不同于O),则△PQR的周长的最小值为 如图,已知:AF、BD、CE、ABC、DEF均是直线,∠EQF=∠APB,∠C=∠D.
如图,已知:AF、BD、CE、ABC、DEF均是直线,∠EQF=∠APB,∠C=∠D.