题目内容
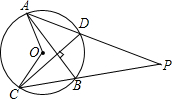如图，AB、CD是⊙O的两条互相垂直的弦，圆心角∠AOC=130°，AD，CB的延长线相交于P，∠P的度数是（ ）| A、20° | B、30° |
| C、40° | D、50° |
考点：圆周角定理
专题：
分析：由圆心角∠AOC=130°，根据圆周角定理，可求得∠ADC与∠ABC的度数，继而求得∠ABP与∠CDP的度数，然后由AB、CD是⊙O的两条互相垂直的弦，求得∠P的度数．
解答：解：∵圆心角∠AOC=130°，
∴∠ADC=∠ABC=
∠AOC=65°，
∴∠ABP=∠CDP=115°，
∵AB⊥CD，
∴∠P=360°-115°-115°-90°=40°．
故选C．
∴∠ADC=∠ABC=
| 1 |
| 2 |
∴∠ABP=∠CDP=115°，
∵AB⊥CD，
∴∠P=360°-115°-115°-90°=40°．
故选C．
点评：此题考查了圆周角定理以及四边形的内角和定理．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图，在矩形铁片ABCE上剪下以A为圆心，AD为半径的扇形，再在余下的部分剪下一个尽可能大的圆形铁片，如果要使这个圆形铁片恰好是扇形铁片所做成的圆锥的底面，那么矩形铁片的长a和宽b应满足什么条件？如图1，水平地面上有一面积为30π平方厘米的灰色扇形OAB，其中OA的长度为6厘米，且与地面垂直．若在没有滑动的情况下，将图1的扇形向右滚动至OB垂直地面为止，如图2所示，则O点移动（ ）厘米．
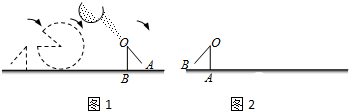
| A、20 | B、24 |
| C、10π | D、30π |
如图，∠AOB是平角，OD平分∠BOC，OE平分∠AOC，那么与∠AOE互余的角有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
如图，△ABC的面积等于25cm2，AE=ED，BD=3DC，则图中阴影部分的面积等于