题目内容
在等腰直角△ABC中,其中AB=AC,∠BAC=90°,过B、C作经过A点直线L的垂线,垂足分别为M、N
(1)BM、CN、MN之间有何数量关系?并说明理由;
(2)若将直线l旋转到如图②的位置,其他条件不变,那么BM、CN、MN之间又有何关系?请说明理由.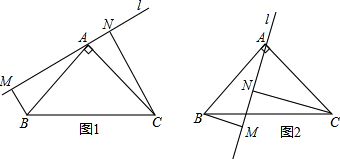
(1)BM、CN、MN之间有何数量关系?并说明理由;
(2)若将直线l旋转到如图②的位置,其他条件不变,那么BM、CN、MN之间又有何关系?请说明理由.

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)易证∠ABM=∠CAN,即可证明△ABM≌△CAN,可得BM=AN,AM=CN,根据MN=AM+AN,即可解题;
(2)易证∠ABM=∠CAN,即可证明△ABM≌△CAN,可得BM=AN,AM=CN,根据MN=AM-AN,即可解题.
(2)易证∠ABM=∠CAN,即可证明△ABM≌△CAN,可得BM=AN,AM=CN,根据MN=AM-AN,即可解题.
解答:证明:(1)∵∠MAB+∠ABM=90°,∠MAB+∠CAN=90°,
∴∠ABM=∠CAN,
在△ABM和△CAN中,
,
∴△ABM≌△CAN(AAS),
∴BM=AN,AM=CN,
∵MN=AM+AN,
∴MN=CN+BM;
(2)∵∠MAB+∠ABM=90°,∠MAB+∠CAN=90°,
∴∠ABM=∠CAN,
在△ABM和△CAN中,
,
∴△ABM≌△CAN(AAS),
∴BM=AN,AM=CN,
∵MN=AM-AN,
∴MN=CN-BM.
∴∠ABM=∠CAN,
在△ABM和△CAN中,
|
∴△ABM≌△CAN(AAS),
∴BM=AN,AM=CN,
∵MN=AM+AN,
∴MN=CN+BM;
(2)∵∠MAB+∠ABM=90°,∠MAB+∠CAN=90°,
∴∠ABM=∠CAN,
在△ABM和△CAN中,
|
∴△ABM≌△CAN(AAS),
∴BM=AN,AM=CN,
∵MN=AM-AN,
∴MN=CN-BM.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABM≌△CAN是解题的关键.

练习册系列答案
相关题目
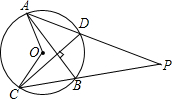 如图,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于P,∠P的度数是( )
如图,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于P,∠P的度数是( )| A、20° | B、30° |
| C、40° | D、50° |
 如图,△ABC≌△DEF,BE=1.3,AE=1,则DE的长是( )
如图,△ABC≌△DEF,BE=1.3,AE=1,则DE的长是( )| A、0.3 | B、1 |
| C、1.3 | D、2.3 |
 如图,把一个三角板绕直角顶点A转动一定的角度,若∠BAE=127°,则∠DAC=
如图,把一个三角板绕直角顶点A转动一定的角度,若∠BAE=127°,则∠DAC= 如图,∠A=∠B,CE∥AD,交AB于点E,CE=10cm,求BC的长度.
如图,∠A=∠B,CE∥AD,交AB于点E,CE=10cm,求BC的长度. 如图所示,已知∠1+∠2=180°,∠B=∠3,请你判断DE和BC平行吗?说明理由.
如图所示,已知∠1+∠2=180°,∠B=∠3,请你判断DE和BC平行吗?说明理由.