题目内容
 如图,在矩形铁片ABCE上剪下以A为圆心,AD为半径的扇形,再在余下的部分剪下一个尽可能大的圆形铁片,如果要使这个圆形铁片恰好是扇形铁片所做成的圆锥的底面,那么矩形铁片的长a和宽b应满足什么条件?
如图,在矩形铁片ABCE上剪下以A为圆心,AD为半径的扇形,再在余下的部分剪下一个尽可能大的圆形铁片,如果要使这个圆形铁片恰好是扇形铁片所做成的圆锥的底面,那么矩形铁片的长a和宽b应满足什么条件?考点:圆锥的计算
专题:
分析:首先求得弧AE的长,然后利用弧AE的长正好等于圆的底面周长,求得⊙O的半径,则BE的长加上半径即为AD的长.
解答: 解:∵AB=b,∠B=90°,
解:∵AB=b,∠B=90°,
∴
=
=
,
设⊙O与AD、CD分别相切于F、G,
连接FO并延长交BC于H,则FH垂直于AD,OG垂直于CD,
可得矩形ABHF、矩形CDFH、矩形CGOH和正方形DFOG,
∴FE⊥BC,
设OG=OF=r,
则2πr=
,
解得:r=
,
∴AD=BC=a=AF+FD=b+
,
整理得:4a=5b.
 解:∵AB=b,∠B=90°,
解:∵AB=b,∠B=90°,∴
 |
| AE |
| 90πb |
| 180 |
| bπ |
| 2 |
设⊙O与AD、CD分别相切于F、G,
连接FO并延长交BC于H,则FH垂直于AD,OG垂直于CD,
可得矩形ABHF、矩形CDFH、矩形CGOH和正方形DFOG,
∴FE⊥BC,
设OG=OF=r,
则2πr=
| bπ |
| 2 |
解得:r=
| b |
| 4 |
∴AD=BC=a=AF+FD=b+
| b |
| 4 |
整理得:4a=5b.
点评:本题考查了圆锥的计算及相切两圆的性质,解题的关键是熟记弧长的计算公式.

练习册系列答案
相关题目
 下列四幅图中是由右图平移得到的是( )
下列四幅图中是由右图平移得到的是( )A、 |
B、 |
C、 |
D、 |
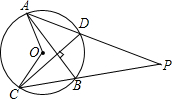 如图,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于P,∠P的度数是( )
如图,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于P,∠P的度数是( )| A、20° | B、30° |
| C、40° | D、50° |
 如图,把一个三角板绕直角顶点A转动一定的角度,若∠BAE=127°,则∠DAC=
如图,把一个三角板绕直角顶点A转动一定的角度,若∠BAE=127°,则∠DAC=