题目内容
13.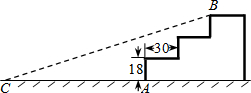 如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )| A. | 270cm | B. | 210cm | C. | 180cm | D. | 96cm |
分析 首先过点B作BD⊥AC于D,根据题意即可求得AD与BD的长,然后由斜坡BC的坡度i=1:5,求得CD的长,继而求得答案.
解答  解:过点B作BD⊥AC于D,
解:过点B作BD⊥AC于D,
根据题意得:AD=2×30=60(cm),BD=18×3=54(cm),
∵斜坡BC的坡度i=1:5,
∴BD:CD=1:5,
∴CD=5BD=5×54=270(cm),
∴AC=CD-AD=270-60=210(cm).
∴AC的长度是210cm.
故答案为:210.
点评 此题考查了解直角三角形的应用:坡度问题.此题难度适中,注意掌握坡度的定义,注意数形结合思想的应用与辅助线的作法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.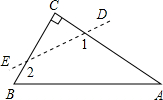 如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
 如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )| A. | 90° | B. | 135° | C. | 150° | D. | 270° |
4.关于x的方程x2+kx-1=0的根的情况描述正确的是( )
| A. | k为任何实数,方程都没有实数根 | |
| B. | k为任何实数,方程都有两个不相等的实数根 | |
| C. | k为任何实数,方程都有两个相等的实数根 | |
| D. | 根据 k 的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
1.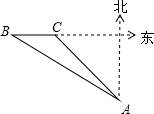 如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )
如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )
 如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )
如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )| A. | (12$\sqrt{2}$+12$\sqrt{6}$)海里/时 | B. | (12$\sqrt{3}$+12$\sqrt{6}$)海里/时 | C. | (12$\sqrt{2}$+12$\sqrt{3}$)海里/时 | D. | (8$\sqrt{3}$+8$\sqrt{6}$)海里/时 |
18.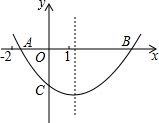 二次函数y=ax2+bx+c的图形如图,OA=OC,下列结论:①abc<0;②4ac<b2;③ac-b<-1;④ac-2a+1>0;⑤OB•OC=-$\frac{c}{a}$.其中结论正确的序号有( )
二次函数y=ax2+bx+c的图形如图,OA=OC,下列结论:①abc<0;②4ac<b2;③ac-b<-1;④ac-2a+1>0;⑤OB•OC=-$\frac{c}{a}$.其中结论正确的序号有( )
 二次函数y=ax2+bx+c的图形如图,OA=OC,下列结论:①abc<0;②4ac<b2;③ac-b<-1;④ac-2a+1>0;⑤OB•OC=-$\frac{c}{a}$.其中结论正确的序号有( )
二次函数y=ax2+bx+c的图形如图,OA=OC,下列结论:①abc<0;②4ac<b2;③ac-b<-1;④ac-2a+1>0;⑤OB•OC=-$\frac{c}{a}$.其中结论正确的序号有( )| A. | ②⑤ | B. | ②④⑤ | C. | ②③④⑤ | D. | ②③⑤ |
5.下列五家银行行标中,既是中心对称图形,又是轴对称图形的个数有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
2. 如图为一根圆柱形的空心钢管,它的主视图是( )
如图为一根圆柱形的空心钢管,它的主视图是( )
 如图为一根圆柱形的空心钢管,它的主视图是( )
如图为一根圆柱形的空心钢管,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
3. 如图是由4个大小相同的正方体搭成的几何体,其左视图是( )
如图是由4个大小相同的正方体搭成的几何体,其左视图是( )
 如图是由4个大小相同的正方体搭成的几何体,其左视图是( )
如图是由4个大小相同的正方体搭成的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
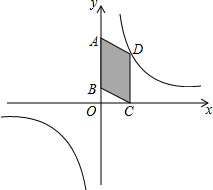 如图,平行四边形ABCD的一边AB在y轴上,顶点C在x轴上,顶点D在双曲线y=$\frac{6}{x}$上,则平行四边形ABCD的面积是( )
如图,平行四边形ABCD的一边AB在y轴上,顶点C在x轴上,顶点D在双曲线y=$\frac{6}{x}$上,则平行四边形ABCD的面积是( )