题目内容
18.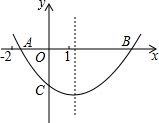 二次函数y=ax2+bx+c的图形如图,OA=OC,下列结论:①abc<0;②4ac<b2;③ac-b<-1;④ac-2a+1>0;⑤OB•OC=-$\frac{c}{a}$.其中结论正确的序号有( )
二次函数y=ax2+bx+c的图形如图,OA=OC,下列结论:①abc<0;②4ac<b2;③ac-b<-1;④ac-2a+1>0;⑤OB•OC=-$\frac{c}{a}$.其中结论正确的序号有( )| A. | ②⑤ | B. | ②④⑤ | C. | ②③④⑤ | D. | ②③⑤ |
分析 根据函数图象可以得到以下信息:a>0,b<0,c<0,再结合函数图象判断各结论.
解答 解:由函数图象可以得到以下信息:a>0,b<0,c<0,
∴abc>0,故错误;
抛物线与x轴有两个交点,b2-4ac>0,
∴4ac<b2,故②正确;
∵OA=OC,
∴A点横坐标等于c,
则ac2+bc+c=0,
则ac+b+1=0,
ac+b=-1故③错误;
④对称轴x=-$\frac{b}{2a}$>1,2a+b<0,
∴-2a-b>0,
∵ac+b=-1,
∴ac=-b-1,
∴ac-2a+1=-b-2a>0,故④正确;
∵OA=OC,
∴OB•OC=OA•OB=|xA•xB|=-$\frac{c}{a}$,故⑤正确;
所以②④⑤;
故选B.
点评 本题考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c系数符号的确定:
(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0.
(2)b由对称轴和a的符号确定:由对称轴公式x=-$\frac{b}{2a}$判断符号.
(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.
(4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.

练习册系列答案
相关题目
8.$\frac{1}{2}$-$\frac{1}{6}$-$\frac{1}{12}$-$\frac{1}{20}$-$\frac{1}{30}$=( )
| A. | $\frac{1}{6}$ | B. | -$\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{6}$ |
9.已知一个样本1,3,2,x,4的平均数是3,则这个样本的方差是( )
| A. | 2 | B. | 2.5 | C. | 10 | D. | $\frac{6}{5}$ |
6.关于x的一元二次方程x2+(m-2)x-2m=0有两个相等的实数根,则m的值是( )
| A. | -2 | B. | 2 | C. | 4+±$\sqrt{2}$ | D. | 0或8 |
13.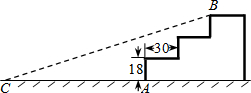 如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
 如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )| A. | 270cm | B. | 210cm | C. | 180cm | D. | 96cm |
7.下列各式中是二次根式的是( )
| A. | $\root{4}{8}$ | B. | $\sqrt{-7}$ | C. | $\sqrt{{a}^{2}+3}$ | D. | $\root{3}{9}$ |
8.在平面直角坐标系中,将点A(-1,1)向右平移5个单位长度得到点B,则点B关于y轴的对称点C的坐标是( )
| A. | (4,1) | B. | (4,-1) | C. | (-4,-1) | D. | (-4,1) |
 如图,直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
如图,直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )


