Question

如图，在平面直角坐标系中放入一张长方形纸片OABC，其中O是坐标原点，OA，OC分别在x轴，y轴的正半轴上，现在纸片沿CE翻折，使点B落在x轴上，记为B′，若OA=15，OC=9，则折痕CE所在直线的解析式为

 

．

Answer 1

考点：翻折变换（折叠问题）,待定系数法求一次函数解析式

专题：

分析：如图，运用勾股定理求出OB′的长度；进而求出AB′的长度；运用勾股定理求出AE的长度；此为解决问题的关键结论；求出C、E两点的坐标，运用待定系数法即可解决问题．

解答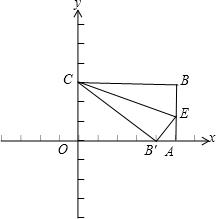：解：∵四边形OABC为正方形，
∴BC=OA=15，∠B=90°，∠B′AE=90°；
由题意得：CB′=CB=15，BE=B′E（设为λ），
由勾股定理得：OB′²=15²-9²，
解得：OB′=12，AB′=15-12=3；
在△AB′E中，由勾股定理得：
λ²=3²+（9-λ）²，
解得：λ=5，EA=9-5=4，
∴C、E两点的坐标为C（0，9）、E（15，4）；
设直线CE的方程为y=kx+b，
则

15k+b=4 b=9

，
解得：k=-

1

3

，b=9；
∴折痕CE所在直线的解析式为y=-

1

3

x+9．
故答案为y=-

1

3

x+9．

点评：该题主要考查了翻折变换、用待定系数法来求一次函数的解析式等数学知识点问题；解题的关键是灵活运用勾股定理等几何知识点求出线段AE的长度．