Question

如图，在Rt△ABC中，∠ACB=90°，且AC=b，BC=a，AB=c，∠A与∠B的平分线交于点O，O到AB的距离为OD．试探究OD与a、b、c的数量关系．

Answer 1

考点：角平分线的性质

专题：

分析：过点O作OE⊥AB于E，OF⊥AC于F，然后根据角平分线上的点到角的两边的距离相等的性质可得OD=OE=OF，然后证得四边形EOFC是正方形，从而证得OE=OF=FC=EC=OD，AE=AD，BD=BF，通过AB=AC-OD+BC-OD即可求得；

解答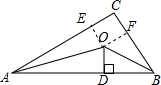：解：：如图，过点O作OE⊥AC于E，OF⊥BC于F，
∵∠BAC、∠ABC的平分线，OD⊥AB，
∴OD=OE，OD=OF，
∴OD=OE=OF，
∵∠ACB=90°，
∴四边形EOFC是正方形，
∴OE=OF=FC=EC=OD，
在RT△OAE和RT△OAD中，

OE=OD OA=OA

，
∴RT△OAE≌RT△OAD（HL），
∴AE=AD，
同理：BD=BF，
∴AE+EC=AD+OD=AC=b，BF+CF=BD+OD=BC=a，
∴AD=b-OD，BD=a-OD，
∴AD+BD=a+b-2OD，即c=a+b-2OD，
∴OD=

1

2

（a+b-c）．

点评：本题主要考查了角平分线上的点到角的两边的距离相等的性质以及正方形的判定和性质，熟记性质是解题的关键．