题目内容
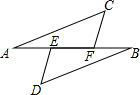 如图,点A,B,E,F在同一直线上,有下列命题:“若AE=BF,∠A=∠B,则△ACF≌△BDE”判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.
如图,点A,B,E,F在同一直线上,有下列命题:“若AE=BF,∠A=∠B,则△ACF≌△BDE”判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.考点:全等三角形的判定,命题与定理
专题:常规题型
分析:根据全等三角形的判定命题“若AE=BF,∠A=∠B,则△ACF≌△BDE”是假真命题,若利用“SAS”判定△ACF≌△BDE,则可添加条件AC=BD.
解答:解:命题“若AE=BF,∠A=∠B,则△ACF≌△BDE”是假真命题,可添加条件AC=BD,使它成为一个真命题.
证明如下:∵AE=BF,
∴AE+EF=BF+EF,
即AF=BE,
在△ACF和△BDE中,
,
∴△ACF≌△BDE(SAS).
证明如下:∵AE=BF,
∴AE+EF=BF+EF,
即AF=BE,
在△ACF和△BDE中,
|
∴△ACF≌△BDE(SAS).
点评:本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.也考查了命题与定理.

练习册系列答案
相关题目
在△ABC中,∠C=90°,AC=15,BC=8,则点C到直线AB的距离是( )
A、
| ||
B、
| ||
| C、8 | ||
| D、15 |
 若有理数a在数轴上对应的点如图所示,则a,-a,-1的大小关系是( )
若有理数a在数轴上对应的点如图所示,则a,-a,-1的大小关系是( )| A、a<-a<-1 |
| B、-a<a<-1 |
| C、-a<-1<a |
| D、a<-1<-a |
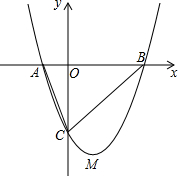 (1)数学小组的单思稿同学认为形如的抛物线y=ax2+bx+c,系数a、b、c一旦确定,抛物线的形状、大小、位置就不会变化,所以称数a、b、c为抛物线y=ax2+bx+c的特征数,记作{a,b,c};请求出与y轴交于点C(0,-3)的抛物线y=x2-2x+k在单同学眼中的特征数;
(1)数学小组的单思稿同学认为形如的抛物线y=ax2+bx+c,系数a、b、c一旦确定,抛物线的形状、大小、位置就不会变化,所以称数a、b、c为抛物线y=ax2+bx+c的特征数,记作{a,b,c};请求出与y轴交于点C(0,-3)的抛物线y=x2-2x+k在单同学眼中的特征数;