题目内容
已知二次函数y=x2-2bx+c的图象与x轴只有一个交点.
(1)请写出b、c的关系式;
(2)设直线y=7与该抛物线的交点为A、B,求AB的长;
(3)若P(a,-a)不在曲线y=x2-2bx+c上,请求出b的取值范围.
(1)请写出b、c的关系式;
(2)设直线y=7与该抛物线的交点为A、B,求AB的长;
(3)若P(a,-a)不在曲线y=x2-2bx+c上,请求出b的取值范围.
考点:抛物线与x轴的交点,二次函数图象上点的坐标特征
专题:
分析:(1)根据二次函数的图象与x轴只有一个交点,则b2-4ac=0,由此可得到b、c应满足关系;
(2)根据根与系数的关系x1+x2=2b,x1x2=c-7,结合b2=c,即可求得AB的长.
(3)由题意可知方程-x=x2-2bx+c没有实数根,根据根的判别式即可求得.
(2)根据根与系数的关系x1+x2=2b,x1x2=c-7,结合b2=c,即可求得AB的长.
(3)由题意可知方程-x=x2-2bx+c没有实数根,根据根的判别式即可求得.
解答:解:(1)∵二次函数y=x2-2bx+c的图象与x轴只有一个交点,
令y=0得:x2-2bx+c=0,
∵△=(-2b)2-4c=0,
∴b2=c.
(2)设A(x1,0),B(x2,0),
∵直线y=7与抛物线的交点A、B的横坐标就是方程x2-2bx+c-7=0的两个根x1、x2.
∴AB=|x1-x2|,
∵x1+x2=2b,x1x2=c-7,b2=c.
∴AB=|x1-x2|=
=
=
=
=2
.
(3)P(a,-a)不在曲线y=x2-2bx+c上,
∴直线y=-x与曲线y=x2-2bx+c没有交点,
即方程-x=x2-2bx+c没有实数根,
∴x2+(1-2b)x+c=0的△<0,
即(1-2b)2-4c<0,
整理得,1-4b+4b2-4c<0,
∵b2=c.
∴1-4b<0,
∴b>
.
令y=0得:x2-2bx+c=0,
∵△=(-2b)2-4c=0,
∴b2=c.
(2)设A(x1,0),B(x2,0),
∵直线y=7与抛物线的交点A、B的横坐标就是方程x2-2bx+c-7=0的两个根x1、x2.
∴AB=|x1-x2|,
∵x1+x2=2b,x1x2=c-7,b2=c.
∴AB=|x1-x2|=
| (x1+x2)2-4x1x2 |
| (2b)2-4(c-7) |
| 4b2-4c+28 |
| 28 |
| 7 |
(3)P(a,-a)不在曲线y=x2-2bx+c上,
∴直线y=-x与曲线y=x2-2bx+c没有交点,
即方程-x=x2-2bx+c没有实数根,
∴x2+(1-2b)x+c=0的△<0,
即(1-2b)2-4c<0,
整理得,1-4b+4b2-4c<0,
∵b2=c.
∴1-4b<0,
∴b>
| 1 |
| 4 |
点评:本题是二次函数的综合题型,主要考查了根的判别式,二次函数与直线的交点问题,二次函数与不等式的关系,题目的综合性较强,难度不小,对学生的解题能力要求很高,是一道不错的中考压轴题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
下列多项式中,不能用公式法因式分解的是( )
| A、x2+xy | ||
| B、x2+2xy+y2 | ||
| C、-x2+y2 | ||
D、
|
 一个几何体的展开图如图所示,则这个几何体是( )
一个几何体的展开图如图所示,则这个几何体是( )| A、三棱锥 | B、四棱锥 |
| C、三棱柱 | D、四棱柱 |
下列代数式满足表中条件的是( )
| x | 0 | 1 | 2 | 3 |
| 代数式的值 | -3 | -1 | 1 | 3 |
| A、x-3 | B、-x-3 |
| C、2x-3 | D、3-2x |
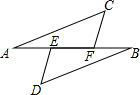 如图,点A,B,E,F在同一直线上,有下列命题:“若AE=BF,∠A=∠B,则△ACF≌△BDE”判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.
如图,点A,B,E,F在同一直线上,有下列命题:“若AE=BF,∠A=∠B,则△ACF≌△BDE”判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明. 如图,开口向上的抛物线y=ax2+bx+c的对称轴是直线x=1,与x轴的一个交点坐标为(-1,0),则当y≥0时,x的取值范围是
如图,开口向上的抛物线y=ax2+bx+c的对称轴是直线x=1,与x轴的一个交点坐标为(-1,0),则当y≥0时,x的取值范围是