题目内容
已知抛物线的顶点坐标是(-1,2),且过点(0,
).
(1)求此抛物线所对应的函数表达式;
(2)求证:对任意实数m,点M(m,-m2)都不在此抛物线上.
| 3 |
| 2 |
(1)求此抛物线所对应的函数表达式;
(2)求证:对任意实数m,点M(m,-m2)都不在此抛物线上.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:
分析:(1)根据抛物线的顶点坐标设出抛物线的顶点形式,将(0,
)代入求出a的值,即可确定出解析式;
(2)把点M(m,-m2)代入二次函数解析式,通过等式左右是否相等判断是否在二次函数图象上.
| 3 |
| 2 |
(2)把点M(m,-m2)代入二次函数解析式,通过等式左右是否相等判断是否在二次函数图象上.
解答:(1)解:∵抛物线顶点坐标(-1,2),
∴设抛物线解析式为y=a(x+1)2+2,
∵抛物线经过点(0,
).
∴a(0+1)2+2=
,
解得:a=-
.
则该抛物线解析式为y=-
(x+1)2+2;
(2)证明:若点M在此二次函数的图象上,
则-m2=-
(m+1)2+2,
得m2-2m+3=0,
方程的判别式:4-12=-8<0,该方程无实根,
所以,对任意实数m,点M(m,-m2)都不在这个二次函数的图象上.
∴设抛物线解析式为y=a(x+1)2+2,
∵抛物线经过点(0,
| 3 |
| 2 |
∴a(0+1)2+2=
| 3 |
| 2 |
解得:a=-
| 1 |
| 2 |
则该抛物线解析式为y=-
| 1 |
| 2 |
(2)证明:若点M在此二次函数的图象上,
则-m2=-
| 1 |
| 2 |
得m2-2m+3=0,
方程的判别式:4-12=-8<0,该方程无实根,
所以,对任意实数m,点M(m,-m2)都不在这个二次函数的图象上.
点评:此题考查了待定系数法求二次函数解析式和图象上的点与解析式的关系,根据判别式△的值得出点是否在函数图象上,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
若抛物线y=x2-2bx+4和x轴只有一个交点,则b的值为( )
| A、2 | B、-2 | C、±2 | D、4 |
下列代数式满足表中条件的是( )
| x | 0 | 1 | 2 | 3 |
| 代数式的值 | -3 | -1 | 1 | 3 |
| A、x-3 | B、-x-3 |
| C、2x-3 | D、3-2x |
关于x的一元二次方程kx2-6x+1=0有两个不相等的实数根,则k的取值范围是( )
| A、k>9 | B、k<9 |
| C、0<k<9 | D、k<9且k≠0 |
下列计算正确的是( )
| A、(x3)2=x5 | ||
| B、x2•x2=x5 | ||
| C、(-2x)3=-8x3 | ||
D、-2a2÷
|
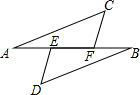 如图,点A,B,E,F在同一直线上,有下列命题:“若AE=BF,∠A=∠B,则△ACF≌△BDE”判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.
如图,点A,B,E,F在同一直线上,有下列命题:“若AE=BF,∠A=∠B,则△ACF≌△BDE”判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.