题目内容
 (1)数学小组的单思稿同学认为形如的抛物线y=ax2+bx+c,系数a、b、c一旦确定,抛物线的形状、大小、位置就不会变化,所以称数a、b、c为抛物线y=ax2+bx+c的特征数,记作{a,b,c};请求出与y轴交于点C(0,-3)的抛物线y=x2-2x+k在单同学眼中的特征数;
(1)数学小组的单思稿同学认为形如的抛物线y=ax2+bx+c,系数a、b、c一旦确定,抛物线的形状、大小、位置就不会变化,所以称数a、b、c为抛物线y=ax2+bx+c的特征数,记作{a,b,c};请求出与y轴交于点C(0,-3)的抛物线y=x2-2x+k在单同学眼中的特征数;(2)同数学小组的尤恪星同学喜欢将抛物线设成y=a(x+m)2+k的顶点式,因此坚持称a、m、k为抛物线的特征数,记作{a,m,k};请求出上述抛物线在尤同学眼中的特征数;
(3)同一个问题在上述两位同学眼中的特征数各不相同,为了让两人的研究保持一致,同组的董和谐将上述抛物线表述成:特征数为{u,v,w}的抛物线沿平行于某轴方向平移某单位后的图象,即此时的特征数{u,v,w}无论按单思稿同学还是按尤恪星同学的理解做出的结果是一样的,请你根据数学推理将董和谐的表述完整地写出来;
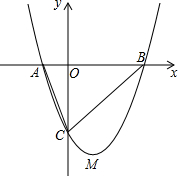
(4)在直角坐标系xOy中,上述(1)中的抛物线与x轴交于A、B两点(A在B的左边),请直接写出△ABC的重心坐标.
考点:二次函数综合题
专题:综合题
分析:(1)把C坐标代入抛物线解析式求出k的值,确定出抛物线解析式,即可得出抛物线在单同学眼中的特征数;
(2)把抛物线解析式化为顶点形式,确定出抛物线在尤同学眼中的特征数即可;
(3)把抛物线解析式化为顶点形式,要使单思稿同学和尤恪星同学的理解做出的结果是一样的,必须满足
,得到b=0,即可得出董和谐的表述;
(4)找出AB的中点,求出AB边中线方程,同理求出AC边中线方程,联立求出重心坐标即可.
(2)把抛物线解析式化为顶点形式,确定出抛物线在尤同学眼中的特征数即可;
(3)把抛物线解析式化为顶点形式,要使单思稿同学和尤恪星同学的理解做出的结果是一样的,必须满足
|
(4)找出AB的中点,求出AB边中线方程,同理求出AC边中线方程,联立求出重心坐标即可.
解答:解:(1)把C(0,-3)代入抛物线解析式得:k=-3,
∴抛物线解析式为y=x2-2x-3,
则该抛物线在单同学眼中的特征数为{1,-2,-3};
(2)∵y=x2-2x-3=(x-1)2-4,
∴上述抛物线在尤同学眼中的特征数为{1,-1,-4};
(3)y=ax2+bx+c=a(x+
)2+c-
,
要使单思稿同学和尤恪星同学的理解做出的结果是一样的,
必须满足
,即b=0,
∵y=(x-1)2-4可以看做y=x2-4沿平行于x轴方向向右平移1个单位而成,
∴董和谐的表述为:特征数{1,0,-4}的抛物线沿平行于x轴方向向右平移1个单位的图象;
(4)对于抛物线解析式y=x2-2x-3,
令y=0,得到x2-2x-3=0,即(x-3)(x+1)=0,
解得:x=3或x=-1,即A(-1,0),B(3,0),C(0,-3),
∴线段AB中点坐标为(1,0),AB边的中线方程为y=
(x-1)=3(x-1)=3x-3;
∵AC边中点坐标为(-
,-
),AC边的中线方程为y=
(x-3)=
(x-3)=
x-
,
联立得:
,
解得:
,
则△ABC的重心坐标为(
,-1).
∴抛物线解析式为y=x2-2x-3,
则该抛物线在单同学眼中的特征数为{1,-2,-3};
(2)∵y=x2-2x-3=(x-1)2-4,
∴上述抛物线在尤同学眼中的特征数为{1,-1,-4};
(3)y=ax2+bx+c=a(x+
| b |
| 2a |
| b2 |
| 4a |
要使单思稿同学和尤恪星同学的理解做出的结果是一样的,
必须满足
|
∵y=(x-1)2-4可以看做y=x2-4沿平行于x轴方向向右平移1个单位而成,
∴董和谐的表述为:特征数{1,0,-4}的抛物线沿平行于x轴方向向右平移1个单位的图象;
(4)对于抛物线解析式y=x2-2x-3,
令y=0,得到x2-2x-3=0,即(x-3)(x+1)=0,
解得:x=3或x=-1,即A(-1,0),B(3,0),C(0,-3),
∴线段AB中点坐标为(1,0),AB边的中线方程为y=
| -3-0 |
| 0-1 |
∵AC边中点坐标为(-
| 1 |
| 2 |
| 3 |
| 2 |
-
| ||
-
|
| 3 |
| 7 |
| 3 |
| 7 |
| 9 |
| 7 |
联立得:
|
解得:
|
则△ABC的重心坐标为(
| 2 |
| 3 |
点评:此题属于二次函数综合题,涉及的知识有:待定系数法求二次函数解析式,线段中点坐标公式,直线的点斜式方程,以及新定义,弄清题中的新定义是解本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 一个几何体的展开图如图所示,则这个几何体是( )
一个几何体的展开图如图所示,则这个几何体是( )| A、三棱锥 | B、四棱锥 |
| C、三棱柱 | D、四棱柱 |
关于x的一元二次方程kx2-6x+1=0有两个不相等的实数根,则k的取值范围是( )
| A、k>9 | B、k<9 |
| C、0<k<9 | D、k<9且k≠0 |
 如图,函数y=
如图,函数y=
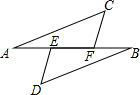 如图,点A,B,E,F在同一直线上,有下列命题:“若AE=BF,∠A=∠B,则△ACF≌△BDE”判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.
如图,点A,B,E,F在同一直线上,有下列命题:“若AE=BF,∠A=∠B,则△ACF≌△BDE”判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.