题目内容
2.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 由于内接正三角形、正方形、正六边形是特殊内角的多边形,可构造直角三角形分别求出边心距的长,由勾股定理逆定理可得该三角形是直角三角形,进而可得其面积.
解答 解:如图1,
∵OC=2,
∴OD=2×sin30°=1;
如图2,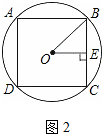
∵OB=2,
∴OE=2×sin45°=$\sqrt{2}$;
如图3,
∵OA=2,
∴OD=2×cos30°=$\sqrt{3}$,
则该三角形的三边分别为:1,$\sqrt{2}$,$\sqrt{3}$,
∵(1)2+($\sqrt{2}$)2=($\sqrt{3}$)2,
∴该三角形是直角边,
∴该三角形的面积是$\frac{1}{2}$×1×$\sqrt{2}$×=$\frac{\sqrt{2}}{2}$,
故选:D.
点评 本题主要考查多边形与圆,解答此题要明确:多边形的半径、边心距、中心角等概念,根据解直角三角形的知识解答是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.某花木公司生产的花卉产品年产量为6万件,每年可通过在网上销售和批发部销售全部售完.该花卉产品平均每件产品的利润与销售的关系如表:
(1)①当网上销售量为4.2万件时,y1=129;y2=120
②y2与x的函数关系为:当0<x≤4时,y2=5x+100;当4≤x<6时,y2=120.
(2)求每年该公司销售这种花卉产品的总利润w(万元)与网上销售数量x(万件)的函数关系式,并指出x的取值范围;
(3)该公司每年网上、批发部的销售量各为多少万件时,可使公司每年的总利润最大?最大值为多少万元?
| 销售量(万件) | 平均每件产品的利润(元) | |
| 网上销售 | x | 当0<x≤2时,y1=140 |
| 当2≤x<6时,y1=-5x+150 | ||
| 批发部销售 | n | 当0<n≤2时,y2=120 |
| 当2≤n<6时,y2=-5n+130 |
②y2与x的函数关系为:当0<x≤4时,y2=5x+100;当4≤x<6时,y2=120.
(2)求每年该公司销售这种花卉产品的总利润w(万元)与网上销售数量x(万件)的函数关系式,并指出x的取值范围;
(3)该公司每年网上、批发部的销售量各为多少万件时,可使公司每年的总利润最大?最大值为多少万元?
10.等腰三角形一边长为2,周长为5,则它的腰长为( )
| A. | 2 | B. | 5 | C. | 1.5 | D. | 1.5或2 |
17.一元二次方程x(x+5)=0的根是( )
| A. | x1=0,x2=5 | B. | x1=0,x2=-5 | C. | x1=0,x2=$\frac{1}{5}$ | D. | x1=0,x2=-$\frac{1}{5}$ |
7.如果用-10%表示某商品的出口额比上一年减少10%,那么+12%则表示该商品的出口额比上一年( )
| A. | 减少12% | B. | 增加12% | C. | 减少22% | D. | 增加2% |
 如图,△ABC中,∠BAC=98°,EF,MN分别为AB,AC的垂直平分线,∠FAN=16°.
如图,△ABC中,∠BAC=98°,EF,MN分别为AB,AC的垂直平分线,∠FAN=16°.