题目内容
11. 如图,△ABC中,∠BAC=98°,EF,MN分别为AB,AC的垂直平分线,∠FAN=16°.
如图,△ABC中,∠BAC=98°,EF,MN分别为AB,AC的垂直平分线,∠FAN=16°.
分析 根据三角形内角和等于180°求出∠B+∠C,再根据线段垂直平分线上的点到线段两端点的距离相等可得AF=BF,AN=CN,根据等边对等角的性质可得∠BAF=∠B,∠CAN=∠C,然后求解即可.
解答 解:∵∠BAC=98°,
∴∠B+∠C=180°-98°=82°,
∵EF,MN分别为AB,AC的垂直平分线,
∴AF=BF,AN=CN,
∴∠BAF=∠B,∠CAN=∠C,
∴∠EAN=∠BAC-(∠BAF+∠CAN)=∠BAC-(∠B+∠C)=98°-82°=16°,
故答案为:16°.
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,三角形内角和定理,等边对等角的性质,整体思想的利用是解题的关键.

练习册系列答案
相关题目
1.下列方程的变形中,正确的是( )
| A. | 若y-4=8,则y=8-4 | |
| B. | 若2(2x-3)=2,则4x-6=2 | |
| C. | 若-$\frac{1}{2}$x=4,则x=-2 | |
| D. | 若 $\frac{1}{3}$-$\frac{t-1}{2}$=1,则去分母得2-3(t-1)=1 |
2.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
19.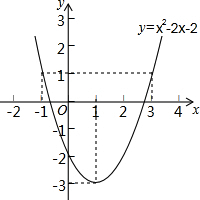 函数y=x2-2x-2的图象如图所示,根据其中提供的信息,可求得使y≤1成立的x的取值范围是( )
函数y=x2-2x-2的图象如图所示,根据其中提供的信息,可求得使y≤1成立的x的取值范围是( )
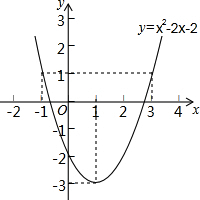 函数y=x2-2x-2的图象如图所示,根据其中提供的信息,可求得使y≤1成立的x的取值范围是( )
函数y=x2-2x-2的图象如图所示,根据其中提供的信息,可求得使y≤1成立的x的取值范围是( )| A. | -1≤x≤3 | B. | -1<x<3 | C. | x<-1或x>3 | D. | x≤-1或x≥3 |
6.下列“QQ表情”中属于轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列运算中,正确的是( )
| A. | (x2)3=x5 | B. | x2+x3=x5 | C. | (x-y)2(y-x)3=(x-y)5 | D. | x2•x3=x5 |
3. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2,AB=20cm,AC=8cm,则DE的长是( )
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2,AB=20cm,AC=8cm,则DE的长是( )
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2,AB=20cm,AC=8cm,则DE的长是( )
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2,AB=20cm,AC=8cm,则DE的长是( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1cm |
