题目内容
10．等腰三角形一边长为2，周长为5，则它的腰长为（ ）| A． | 2 | B． | 5 | C． | 1.5 | D． | 1.5或2 |
分析 分别从若等腰三角形的腰长为2与若等腰三角形的底边长为2去分析求解即可求得答案．
解答 解：若等腰三角形的腰长为2，
则底边长为：5-2-2=1，
∵2+1＞2，
能组成三角形，
此时它的腰长为2；
若等腰三角形的底边长为2，
则腰长为：$\frac{5-2}{2}$=1.5，
∵1.5+1.5＞2，
能组成三角形，
此时它的腰长为1.5．
∴它的腰长为1.5或2．
故选D．
点评 此题考查了等腰三角形的性质以及三角形的三边关系．此题难度不大，注意掌握分类讨论思想的应用．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
7．使一元二次方程x2+3x+m=0有整数根的非负整数m的个数为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
1．下列方程的变形中，正确的是（ ）
| A． | 若y-4=8，则y=8-4 | |
| B． | 若2（2x-3）=2，则4x-6=2 | |
| C． | 若-$\frac{1}{2}$x=4，则x=-2 | |
| D． | 若 $\frac{1}{3}$-$\frac{t-1}{2}$=1，则去分母得2-3（t-1）=1 |
18．
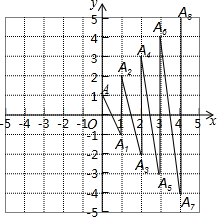如图在平面直角坐标系上有一点A（0，1），点A第一次跳动至点A1（1，-1），第二次由点 A1跳到点A2（1，2），第三次由点A2跳到A3（2，-2）…由此规律跳动下去，第80次跳到点A80的坐标是（ ）
如图在平面直角坐标系上有一点A（0，1），点A第一次跳动至点A1（1，-1），第二次由点 A1跳到点A2（1，2），第三次由点A2跳到A3（2，-2）…由此规律跳动下去，第80次跳到点A80的坐标是（ ）| A． | （40，40） | B． | （41，40） | C． | （40，41） | D． | （41，41） |
5．已知二次函数y=ax2+bx+c中，函数值y与自变量x的部分对应值如表：
则当y＞0时，x的取值范围是-1＜x＜3．
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 3 | 4 | 3 | … |
在△ABC中，AB=8，BC=10，AC=6，动点P从点C出发，沿着CB运动，速度为每秒2个单位，到达点B时运动停止，设运动时间为t秒，请解答下列问题：
2．以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（ ）
| A． | $\frac{\sqrt{3}}{4}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{2}}{4}$ | D． | $\frac{\sqrt{2}}{2}$ |
19．
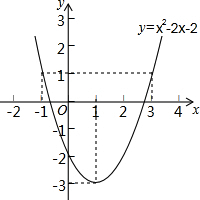函数y=x2-2x-2的图象如图所示，根据其中提供的信息，可求得使y≤1成立的x的取值范围是（ ）
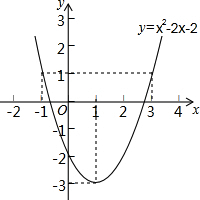函数y=x2-2x-2的图象如图所示，根据其中提供的信息，可求得使y≤1成立的x的取值范围是（ ）| A． | -1≤x≤3 | B． | -1＜x＜3 | C． | x＜-1或x＞3 | D． | x≤-1或x≥3 |