题目内容
15. 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.(1)请用直尺和圆规在边AC上作一点P,且使PA=PB(不写作法,保留作图痕迹);
(2)当∠B=60度时,PA:PC=2:1.
分析 (1)作AB的垂直平分线交AC于点P,则PA=PB;
(2)利用PA=PB,PA:PC=2:1得到PB:PC=2:1,则在Rt△BCP中利用余弦的定义可计算出∠BPC=60°,再利用等腰三角形的性质和三角形外角性质可计算出∠A=30°,然后•利用互余计算∠ABC的度数.
解答 解:(1)如图,点P为所作;
(2)∵PA=PB,PA:PC=2:1,
∴PB:PC=2:1,
在Rt△BCP中,∵cos∠BPC=$\frac{PC}{PB}$=$\frac{1}{2}$,
∴∠BPC=60°,
∵PA=PB,
∴∠A=∠PBA,
∵∠BPC=∠A+∠PBA,
∴∠A=30°,
∴∠ABC=60°.
故答案为60.
点评 本题考查了基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.解决(2)小题的关键是利用三角函数确定∠BPC的度数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下面说法正确的是( )
| A. | $\frac{1}{4}$和-4互为相反数 | B. | $\frac{1}{4}$和-4互为倒数 | ||
| C. | 0.1和10互为倒数 | D. | 0的倒数是0 |
6.已知一元二次方程x2+3x+2=0,下列判断正确的是( )
| A. | 该方程无实数解 | B. | 该方程有两个相等的实数解 | ||
| C. | 该方程有两个不相等的实数解 | D. | 该方程解的情况不确定 |
10.将平面直角坐标系中的点A(2,1)向左平移2个单位长度,再向下平移4个单位长度得到点A′,若将点A到A′的平移看作一次平移,则平移的距离为( )
| A. | 6个单位长度 | B. | 4个单位长度 | C. | 2个单位长度 | D. | 2$\sqrt{5}$个单位长度 |
4. 如图,直线l1∥l2,∠A=124°,∠B=86°,则∠1+∠2=( )
如图,直线l1∥l2,∠A=124°,∠B=86°,则∠1+∠2=( )
 如图,直线l1∥l2,∠A=124°,∠B=86°,则∠1+∠2=( )
如图,直线l1∥l2,∠A=124°,∠B=86°,则∠1+∠2=( )| A. | 30° | B. | 35° | C. | 36° | D. | 40° |
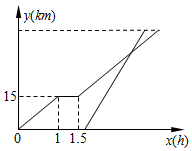 周末,小华骑自行车从家出发到植物园玩,从家出发1小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华从家出发1小时50分后,爸爸从家出发骑摩托车沿相同路线前往植物园,如图是他们家的路程y(km)与小华离家的时间x(h)的函数图象,已知爸爸骑摩托车的速度是小华骑车速度的2倍,若爸爸比小华早10分达到植物园,则小华家到植物园的路程是45km.
周末,小华骑自行车从家出发到植物园玩,从家出发1小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华从家出发1小时50分后,爸爸从家出发骑摩托车沿相同路线前往植物园,如图是他们家的路程y(km)与小华离家的时间x(h)的函数图象,已知爸爸骑摩托车的速度是小华骑车速度的2倍,若爸爸比小华早10分达到植物园,则小华家到植物园的路程是45km.