已知:$\frac{x}{3}$=$\frac{y}{4}$=$\frac{z}{6}$.那么$\frac{3x+2y}{4z-2x}$=$\frac{17}{18}$．题目和参考答案——青夏教育精英家教网—

题目内容

7．已知：$\frac{x}{3}$=$\frac{y}{4}$=$\frac{z}{6}$，那么$\frac{3x+2y}{4z-2x}$=$\frac{17}{18}$．

分析设$\frac{x}{3}$=$\frac{y}{4}$=$\frac{z}{6}$=k，利用比例性质得x=3k，y=4k，z=6k，然后把它们代入$\frac{3x+2y}{4z-2x}$中进行分式的运算即可．

解答解：设$\frac{x}{3}$=$\frac{y}{4}$=$\frac{z}{6}$=k，
则x=3k，y=4k，z=6k，
所以$\frac{3x+2y}{4z-2x}$=$\frac{9k+8k}{24k-6k}$=$\frac{17}{18}$．
故答案为$\frac{17}{18}$．

点评本题考查了比例的性质：常用的性质有内项之积等于外项之积；合比性质；分比性质；合分比性质；等比性质．

练习册系列答案

相关题目

17．在△ABC中，AC=5，AB=7，则中线AD的范围是0＜AD＜6．

18．

在△ABC中，点D是BC的中点．
（1）过点C和点B分别作CE⊥AD，BF⊥AD，垂足分别为E，F；
（2）请证明：BF=CE．

15．已知x=$\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}-\sqrt{3}}$，y=$\frac{\sqrt{2}-\sqrt{3}}{\sqrt{2}+\sqrt{3}}$，求x²-5xy+y²的值．

2．

已知：如图，△ABCD的对角线AC，BD相交于点O，点E，F分别在AO，CO上，且AE=CF，求证：∠EBO=∠FDO．

12．在中国经济新常态下，某公司销售收入节节攀升，季度实现销售收入共计1600万元，其中二月份的销售收入是一月份的2倍，三月份的销售收入是二月份的2.5倍，则一月份的销售收入为200万元．

7．

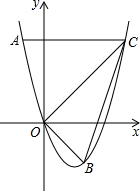如图，二次函数y=x²+bx的图象经过点A（-1，4）和点B（2，m）．
（1）填空：b=-3；m=-2；
（2）过点A作AC∥x轴，交抛物线于点C，点P是线段OC上的动点（与O、C不重合）．
①若以O、B、C为顶点的三角形和以O、B、P为顶点的三角形相似，求它们的相似比；
②设点F是BC的中点，当OP为何值时，将△BPF沿边PF翻折，使△BPF与△CPF重叠部分的面积是△BCP的面积的$\frac{1}{4}$？

4．（1）若一个数的平方根为2a+3和a-9，则这个数是49．
（2）若$\sqrt{10}$的整数部分是a，小数部分是b，则${（b-\sqrt{10}）^a}$=-27．

5．

如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE 的中点，且S_△ABC=8cm²，则S_阴影面积等于（　　）

试题分类