题目内容
7.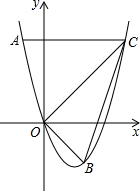 如图,二次函数y=x2+bx的图象经过点A(-1,4)和点B(2,m).
如图,二次函数y=x2+bx的图象经过点A(-1,4)和点B(2,m).(1)填空:b=-3;m=-2;
(2)过点A作AC∥x轴,交抛物线于点C,点P是线段OC上的动点(与O、C不重合).
①若以O、B、C为顶点的三角形和以O、B、P为顶点的三角形相似,求它们的相似比;
②设点F是BC的中点,当OP为何值时,将△BPF沿边PF翻折,使△BPF与△CPF重叠部分的面积是△BCP的面积的$\frac{1}{4}$?
分析 (1)直接将A点代入求出b的值,再将B点代入求出m的值;
(2)①若以O、B、C为顶点的三角形和以O、B、P为顶点的三角形相似,只能是△OBC∽△OCP,进而求出相似比;
②1)分别利用若翻折后,点B′落在BC的右侧,2)若翻折后,点B′落在BC上,则点B,D重合,3)若翻折后,点B落在OC的左侧,分别得出答案.
解答 解:(1)∵二次函数y=x2+bx的图象经过点A(-1,4)和点B(2,m),
∴4=(-1)2-b,
解得:b=-3,
则m=22-3×2=-2,
故答案为:-3,-2;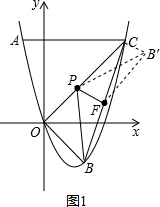
(2)过点A作AC∥x轴,交抛物线于点C,
即4=x2-3x,
解得:x1=-1,x2=4,
可得C(4,4),又∵B(2,-2),
∴∠COB=90°,
①若以O、B、C为顶点的三角形和以O、B、P为顶点的三角形相似,
只能是△OBC∽△OCP,
∴△OBC与△OPB的相似比为:OC:OB=2:1;
②由①知CO=4$\sqrt{2}$,BO=2$\sqrt{2}$,BF=FC=$\sqrt{10}$.
1)若翻折后,点B′落在BC的右侧,BC与PB′的交点为M,如图1.
S△MFP=$\frac{1}{4}$S△BCP=$\frac{1}{2}$S△CPF=$\frac{1}{2}$S△B′PF,
∴M为FC、PB′的中点
∴四边形B′FPC为平行四边形,
∴PC=$\sqrt{10}$,PO=4$\sqrt{2}$-$\sqrt{10}$,
2)若翻折后,点B′落在BC上,则点B,D重合,
S△MFP=$\frac{1}{2}$S△BCP,不合题意,舍去.
3)若翻折后,点B落在OC的左侧,
OC与FB′的交点为N,如图2,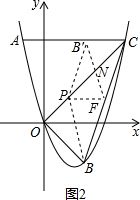 S△NPF=$\frac{1}{4}$S△BCP=$\frac{1}{2}$S△BPF=$\frac{1}{2}$S△CPF=$\frac{1}{2}$S△B′PF,
S△NPF=$\frac{1}{4}$S△BCP=$\frac{1}{2}$S△BPF=$\frac{1}{2}$S△CPF=$\frac{1}{2}$S△B′PF,
∴N为PC、FB′的中点,
∴四边形B′PFC为平行四边形,
B′P=FC=$\sqrt{10}$,∴BP=B′P=$\sqrt{10}$,
在直角三角形OPB中,
OP2+OB2=BP2,
解得:PO=$\sqrt{2}$,
综上所述,PO=4$\sqrt{2}$-$\sqrt{10}$或PO=$\sqrt{2}$.
点评 此题主要考查了二次函数综合以及相似三角形的判定与性质和平行四边形的判定与性质等知识,正确利用分类讨论以及数形结合得出答案是解题关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案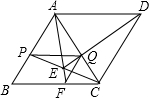 如图,在菱形ABCD中,AC=AB,P是AB边上的任意一点(点P与A,B两点不重合),PQ∥BC交AC于点Q,DQ的延长线交PC于点E,AE的延长线交BC于点F,连接FQ,则下列结论错误的是( )
如图,在菱形ABCD中,AC=AB,P是AB边上的任意一点(点P与A,B两点不重合),PQ∥BC交AC于点Q,DQ的延长线交PC于点E,AE的延长线交BC于点F,连接FQ,则下列结论错误的是( )| A. | FQ∥AB | B. | AQ=BF | ||
| C. | ∠PEF=120° | D. | DE不是∠AEC的平分线 |
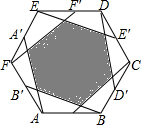 如图,正六边形ABCDEF的面积为2009,A′至F′为各边中点,顺次连接AA′至FF′,求阴影六边形的面积.
如图,正六边形ABCDEF的面积为2009,A′至F′为各边中点,顺次连接AA′至FF′,求阴影六边形的面积.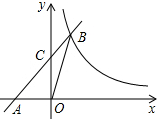 直线y=kx+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则m的值是( )
直线y=kx+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则m的值是( )