题目内容
2. 已知:如图,△ABCD的对角线AC,BD相交于点O,点E,F分别在AO,CO上,且AE=CF,求证:∠EBO=∠FDO.
已知:如图,△ABCD的对角线AC,BD相交于点O,点E,F分别在AO,CO上,且AE=CF,求证:∠EBO=∠FDO.
分析 连接DE、BF,由平行四边形的性质得出OB=OD,OA=OC,由已知条件得出OE=OF,证明四边形BEDF是平行四边形,得出对边平行BE∥DF,即可得出结论.
解答 证明:连接DE、BF,如图所示:
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵AE=CF,
∴OE=OF,
∴四边形BEDF是平行四边形,
∴BE∥DF,
∴∠EBO=∠FDO.
点评 本题考查了平行四边形的判定与性质、平行线的性质;熟练掌握平行四边形的判定与性质,证明四边形BEDF是平行四边形是解决问题的关键.

练习册系列答案
相关题目
13.某工厂本周内计划每日生产300辆电动车,由于每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数):
(1)本周三生产了多少辆电动车?
(2)本周总生产量是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(2)本周总生产量是多少?
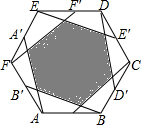 如图,正六边形ABCDEF的面积为2009,A′至F′为各边中点,顺次连接AA′至FF′,求阴影六边形的面积.
如图,正六边形ABCDEF的面积为2009,A′至F′为各边中点,顺次连接AA′至FF′,求阴影六边形的面积.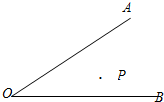 如图,已知∠AOB,P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点,
如图,已知∠AOB,P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点,