题目内容

18．若a是整数，且分式$\frac{2a-7}{a-2}$的值是正整数，试求出a的值．

分析 设$\frac{2a-7}{a-2}$=k，通过整理得出a=$\frac{7-2k}{2-k}$，再根据分式$\frac{2a-7}{a-2}$的值是正整数，求出k的值，再代入计算即可求出a．

解答 解：设$\frac{2a-7}{a-2}$=k，则2a-7=k（a-2），
整理得：a=$\frac{7-2k}{2-k}$，
∵k是正整数，a只是整数，
∴k=5时，a=1，k=3时，a=-1，k=1时，a=5．

点评 本题考查了分式的值，认真审题，抓住关键的字眼，是正确解题的出路；如本题“整数a”中的“整数”，“$\frac{2a-7}{a-2}$的值为正整数”中的“正整数”．

练习册系列答案
相关题目
8．求下列函数的定义域：
（1）y=x2+x；
（2）y=$\frac{2+x}{2-x}$；
（3）y=$\sqrt{3-2x}$；
（4）y=$\frac{1}{\sqrt{2+3x}}$．
9．不解方程，求下列方程两根x1，x2的和与积．
（1）x2-3x+1=0
（2）2x2+5x+1=0
（3）2x2+5x=0
（4）x2-8=0．
6．下面是甲、乙两位同学对两个问题的解答，请判断正误，并说明你的理由．
甲同学：当x取何值时．分式$\frac{{x}^{2}-1}{（x-1）（x+2）}$的值为零？
解：当分子x2-1=0时，即x=±1时，分式$\frac{{x}^{2}-1}{（x-1）（x+2）}$的值为零．
乙同学：若分式$\frac{1}{1-\frac{1}{|x|}}$有意义，求x的取值范围．
解：当|x|≠0，即x≠0时，分式有意义，所以x的取值范围是x≠0．
13．把二次函数y=-2x2的图象向右平移1个单位．
（1）写出平移后的函数解析式；
（2）求出平移后的函数图象的顶点坐标，对称轴．
3．阅读并计算：例：计算：$\frac{1}{x（x+1）}$+$\frac{1}{（x+1）（x+2）}$+$\frac{1}{（x+2）（x+3）}$．原式=$\frac{1}{x}$-$\frac{1}{x+1}$+$\frac{1}{x+1}$-$\frac{1}{x+2}$+$\frac{1}{x+2}$-$\frac{1}{x+3}$=$\frac{1}{x}$-$\frac{1}{x+3}$=$\frac{3}{x（x+3）}$．
仿照上例计算：$\frac{2}{x（x+2）}$+$\frac{2}{（x+2）（x+4）}$+$\frac{2}{（x+4）（x+6）}$．
10．要使y=（m-2）xn-1+n是关于x的一次函数，则m，n应满足n=2，m≠2．
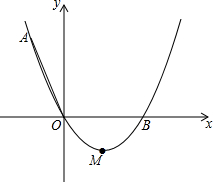13．如图，在平面直角坐标系xOy中，顶点为M的抛物线y=ax2+bx（a＞0）经过点A和x轴正半轴上的点B，AO=OB=4，∠AOB=120°．
（1）求这条抛物线的表达式；
（2）联结OM，求∠AOM的大小；
（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．
14．下列能构成直角三角形三边长的是（　　）
①2、3、4      ②3、4、5      ③15、20、25      ④7、24、25．
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网