题目内容
9.解下列不等式组:(1)$\left\{\begin{array}{l}{1+2x>3+x}\\{5x<4x-1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2-x<-1}\\{3<x-1}\end{array}\right.$
(3)$\left\{\begin{array}{l}{\frac{1}{2}+\frac{2x}{3}<\frac{-x}{2}+\frac{5}{3}}\\{3(x-1)<x-5}\end{array}\right.$
(4)$\left\{\begin{array}{l}{\frac{1}{2}(x+3)<2}\\{\frac{x+2}{2}>\frac{x+3}{3}}\end{array}\right.$.
分析 (1)、(2)分别求出各不等式的解集,再求出其公共解集即可;
(3)、(4)先将不等式组的不等式化为不含分母及括号的不等式,分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)$\left\{\begin{array}{l}1+2x>3+x①\\ 5x<4x-1②\end{array}\right.$,由①得,x>2,由②得,x<-1,
故不等式组的解集为空集.
(2)$\left\{\begin{array}{l}2-x<-1①\\ 3<x-1②\end{array}\right.$,由①得,x>3,由②得,x>4,
故不等式组的解集为:x>4.
(3)不等式组可化为$\left\{\begin{array}{l}3+4x<-3x+10①\\ 3x-3<x-5②\end{array}\right.$,由①得,x<1,由②得,x<-1,
故不等式组的解集为:x<-1.
(4)不等式组可化为$\left\{\begin{array}{l}x+3<4①\\-x>-2②\end{array}\right.$,由①得,x<1,由②得,x<2,
故不等式组的解集为:x<1.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
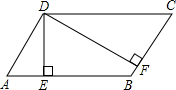 如图,在平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若ABCD的周长为45,DE=5,DF=10,求平行四边形ABCD的面积.
如图,在平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若ABCD的周长为45,DE=5,DF=10,求平行四边形ABCD的面积.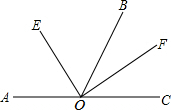 如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.
如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.
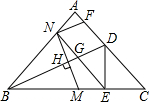 如图,在等腰Rt△ABC中,AB=AC,∠BAC=90°,D为AC上一点,沿BD折叠△ABC,使A点落在BC边上的点E处,M为边BC的中点,MN⊥BD与点H,N在AB边上,连接NE交BD于点G,过点N作BD的平行线交AC于点F,下列结论:①AB=$\sqrt{2}$BN;②四边形DFNG为平行四边形;③△BMN∽△EDG;④AN=DF.其中正确结论的个数是( )
如图,在等腰Rt△ABC中,AB=AC,∠BAC=90°,D为AC上一点,沿BD折叠△ABC,使A点落在BC边上的点E处,M为边BC的中点,MN⊥BD与点H,N在AB边上,连接NE交BD于点G,过点N作BD的平行线交AC于点F,下列结论:①AB=$\sqrt{2}$BN;②四边形DFNG为平行四边形;③△BMN∽△EDG;④AN=DF.其中正确结论的个数是( )