题目内容
19.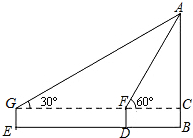 某同学利用测角仪及卷尺测量某校旗杆的高度,在测量中获得了一些数据,并以此画出了如图所示的示意图,已知该同学使用的测角仪(离地面的高度)支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测到旗杆顶端A的仰角为30°,求旗杆的高度.(结果保留根号)
某同学利用测角仪及卷尺测量某校旗杆的高度,在测量中获得了一些数据,并以此画出了如图所示的示意图,已知该同学使用的测角仪(离地面的高度)支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测到旗杆顶端A的仰角为30°,求旗杆的高度.(结果保留根号)
分析 首先证明AF=GF=ED=12,在Rt△ACF中,利用锐角三角函数定义求出AC的长,由AC+BC求出AB的长即可.
解答 解:∵∠AFC=60°,
∴∠AFG=120°,
∵∠CGA=30°,
∴∠GAF=30°,
∴FA=FG=ED=12m,
在Rt△ACF中,AC=AF•sin60°=6$\sqrt{3}$(m),
∵BC=FD=1,
∴AB=AC+BC=(6$\sqrt{3}$+1)m.
点评 此题考查了解直角三角形的应用-仰角俯角问题,等腰三角形的判定和性质、锐角三角函数等知识,解本题的关键发现AF=GF=DE=12,属于中考常考题型.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
9.已知⊙O的半径为1,圆心O的坐标为(0,0),点P的坐标为($\sqrt{2}$,-1),则点P与⊙O的位置关系是( )
| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 点P在⊙O上或⊙O外 |
14.某小学为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
| A. | 平均数是15 | B. | 众数是10 | C. | 中位数是17 | D. | 方差是$\frac{44}{3}$ |
 如图,AB=AC,BD=CE,用无刻度的直尺画出∠A的平分线.
如图,AB=AC,BD=CE,用无刻度的直尺画出∠A的平分线.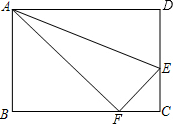 如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,AE为折痕.已知AB=8,BC=10,则EC的长为3.
如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,AE为折痕.已知AB=8,BC=10,则EC的长为3.