题目内容
数轴上点A对应的数为a,点B对应的数为b,且a、b满足a+5=(-1)3,3b+1=3+2b
(1)求a、b.
(2)点P对应的数为x,若点P在A、B之间,请化简|x+8|-|x-2|+|2x-6|.
(3)在线段AB之间有两点C、D,且CD=2,点M为AD的中点,N为BC的中点,求线段MN的长.
(1)求a、b.
(2)点P对应的数为x,若点P在A、B之间,请化简|x+8|-|x-2|+|2x-6|.
(3)在线段AB之间有两点C、D,且CD=2,点M为AD的中点,N为BC的中点,求线段MN的长.
考点:两点间的距离,数轴,绝对值
专题:
分析:(1)根据解方程,可得a、b的值,
(2)根据正数的绝对值等于它的本身,差的绝对值是大数减小数,可化简绝对值,根据整式的加减,可得答案;
(3)根据线段中点的性质,可得MD,CN,根据线段的和差,可得DN,再根据线段的和差,可得答案.
(2)根据正数的绝对值等于它的本身,差的绝对值是大数减小数,可化简绝对值,根据整式的加减,可得答案;
(3)根据线段中点的性质,可得MD,CN,根据线段的和差,可得DN,再根据线段的和差,可得答案.
解答:解:(1)a+5=(-1)3,3b+1=3+2b,解得a=-6,b=2;
(2)由点P在A、B之间,得-6<x<2,
|x+8|-|x-2|+|2x-6|=x+8-(2-x)+(6-2x)=x+8-2+x+6-2x=12;
(3)由点M为AD的中点,N为BC的中点,得
MD=
AD,CN=
BC,
由线段的和差ND=NC-CD,BC=BD+ND,
MN=MD+ND=
AD+NC-CD=
AD+
BC-CD
=
AD+
CD+
BD-CD
=
(AD+BD)-
CD
=4-1=3
(2)由点P在A、B之间,得-6<x<2,
|x+8|-|x-2|+|2x-6|=x+8-(2-x)+(6-2x)=x+8-2+x+6-2x=12;
(3)由点M为AD的中点,N为BC的中点,得
MD=
| 1 |
| 2 |
| 1 |
| 2 |
由线段的和差ND=NC-CD,BC=BD+ND,
MN=MD+ND=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=4-1=3
点评:本题考查了两点间的距离,(1)利用了解方程,(2)利用了绝对值的性质,(3)利用线段的和差ND=NC-CD,BC=BD+ND,MN=MD+ND是解题关键.

练习册系列答案
相关题目
 受国际炒家炒作的影响,今年棉花价格出现了大幅度波动,1至3月份,棉价大幅度上涨,其价格y1(元/吨)与月份x之间的函数关系式:y1=2200x+24200(1≤x≤3,且x取整数).而从4月份起,棉价大幅度走低,其价格y2(元/吨)与月份x(4≤x≤6,且x取整数)之间的函数关系如图所示.
受国际炒家炒作的影响,今年棉花价格出现了大幅度波动,1至3月份,棉价大幅度上涨,其价格y1(元/吨)与月份x之间的函数关系式:y1=2200x+24200(1≤x≤3,且x取整数).而从4月份起,棉价大幅度走低,其价格y2(元/吨)与月份x(4≤x≤6,且x取整数)之间的函数关系如图所示.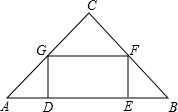 如图,在直角△ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=4,BC=3.
如图,在直角△ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=4,BC=3.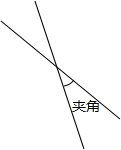 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的“夹角”(见图)现在平面上有若干条直线,它们两两相交并且“夹角”只能是30°或者是60°或者是90°时,问:平面上最多有多少条直线?当直线条数最多时,所有的“夹角”的和是多少?
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的“夹角”(见图)现在平面上有若干条直线,它们两两相交并且“夹角”只能是30°或者是60°或者是90°时,问:平面上最多有多少条直线?当直线条数最多时,所有的“夹角”的和是多少?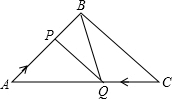 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒. 正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.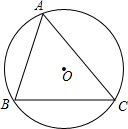 如图,圆O是锐角△ABC的外接圆,其半径为R.BC=a,AC=b,AB=c.求证:
如图,圆O是锐角△ABC的外接圆,其半径为R.BC=a,AC=b,AB=c.求证: