题目内容
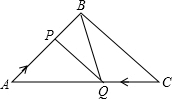 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.(1)x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由;
(3)当
| S△BCQ |
| S△ABC |
| 1 |
| 3 |
| S△APQ |
| S△ABQ |
考点:相似三角形的判定与性质
专题:动点型
分析:(1)当PQ∥BC时,根据平行线分线段成比例定理,可得出关于AP,PQ,AB,AC的比例关系式,我们可根据P,Q的速度,用时间x表示出AP,AQ,然后根据得出的关系式求出x的值.
(2)由△APQ∽△CQB 得出
=
,进一步代入求x的值;
(3)当
=
时得出CQ:AC=1:3,那么CQ=10cm,此时时间x正好是(1)的结果,那么此时PQ∥BC,由此可根据平行这个特殊条件,得出三角形APQ和ABC的面积比,然后再根据三角形PBQ的面积=三角形ABC的面积-三角形APQ的面积-三角形BQC的面积来得出答案即可.
(2)由△APQ∽△CQB 得出
| AP |
| CQ |
| AQ |
| CB |
(3)当
| S△BCQ |
| S△ABC |
| 1 |
| 3 |
解答:解:(1)由题意知 AP=4x,CQ=3x
若PQ∥BC 则△APQ∽△ABC,
=
,
∵AB=BC=20,AC=30,
∴AQ=30-3x,
∴
=
,
∴x=
,
∴当x=
时,PQ∥BC.
(2)存在
∵△APQ∽△CQB 则
=
,
∴
=
,
∴9x2-10x=0,
∴x1=0(舍去).x2=
.
∴当AP的长为
时,△APQ∽△CQB,
(3)∵
=
,
∴
=
,
又∵AC=30,
∴CQ=10,
即3x=10x=
,
此时,AP=4x=
,
∴
=
=
.
∴
=
=
.
若PQ∥BC 则△APQ∽△ABC,
| AP |
| AB |
| AQ |
| AC |
∵AB=BC=20,AC=30,
∴AQ=30-3x,
∴
| 4x |
| 20 |
| 30-3x |
| 30 |
∴x=
| 10 |
| 3 |
∴当x=
| 10 |
| 3 |
(2)存在
∵△APQ∽△CQB 则
| AP |
| CQ |
| AQ |
| CB |
∴
| 4x |
| 3x |
| 30-3x |
| 20 |
∴9x2-10x=0,
∴x1=0(舍去).x2=
| 10 |
| 9 |
∴当AP的长为
| 10 |
| 9 |
(3)∵
| S△BCQ |
| S△ABC |
| 1 |
| 3 |
∴
| CQ |
| AC |
| 1 |
| 3 |
又∵AC=30,
∴CQ=10,
即3x=10x=
| 10 |
| 3 |
此时,AP=4x=
| 40 |
| 3 |
∴
| AP |
| AB |
| ||
| 20 |
| 2 |
| 3 |
∴
| S△APQ |
| S△ABQ |
| AP |
| AB |
| 2 |
| 3 |
点评:本题主要考查了相似三角形的判定和性质,根据三角形相似得出线段比或面积比是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
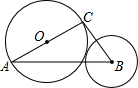 已知,如图,△ABC中,∠C=90,AC=12,BC=8,AC为⊙O的直径,⊙B的半径长为4.求证:⊙O与⊙B外切.
已知,如图,△ABC中,∠C=90,AC=12,BC=8,AC为⊙O的直径,⊙B的半径长为4.求证:⊙O与⊙B外切. 如图,点C为线段AB上一点,D为AC的中点,点E为线段BD的中点.
如图,点C为线段AB上一点,D为AC的中点,点E为线段BD的中点.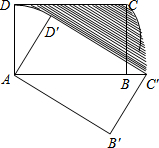 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=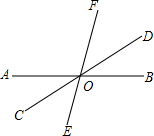 如图,已知直线AB,CD,EF相交于点O,∠COE:∠BOE=2:7,∠BOD=30°,求∠BOF的度数.
如图,已知直线AB,CD,EF相交于点O,∠COE:∠BOE=2:7,∠BOD=30°,求∠BOF的度数.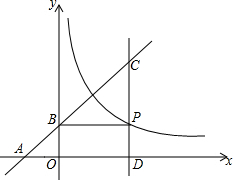 如图,直线y=x+m分别交坐标轴于A、B两点,且交平行于y轴的直线CD:x=n于点C;过点B作BP⊥CD,垂足为P.已知△OAB与△BPC的面积和为30,四边形OBPD的周长为20.若点P为反比例函数y=
如图,直线y=x+m分别交坐标轴于A、B两点,且交平行于y轴的直线CD:x=n于点C;过点B作BP⊥CD,垂足为P.已知△OAB与△BPC的面积和为30,四边形OBPD的周长为20.若点P为反比例函数y= 如图,请你数出五角星中同旁内角的对数.
如图,请你数出五角星中同旁内角的对数.