题目内容
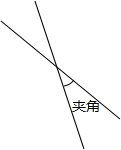 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的“夹角”(见图)现在平面上有若干条直线,它们两两相交并且“夹角”只能是30°或者是60°或者是90°时,问:平面上最多有多少条直线?当直线条数最多时,所有的“夹角”的和是多少?
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的“夹角”(见图)现在平面上有若干条直线,它们两两相交并且“夹角”只能是30°或者是60°或者是90°时,问:平面上最多有多少条直线?当直线条数最多时,所有的“夹角”的和是多少?考点:对顶角、邻补角
专题:
分析:根据题意,“夹角”只能是30°,60°或90°,都是30°的倍数,根据这个倍数,通过旋转的方法,进一步解答即可.
解答:解:因为夹角只能是30°、60°或者90°,其均为30°的倍数,所以每画一条直线后,逆时针旋转30°画下一条直线,这样就能够保证两两直线夹角为30°的倍数,即为30°、60°或者90°(因为如果每次旋转度数其他角度,例如15°,则必然会出现两条直线的夹角为15°或15°的其它倍数,如45°这与题目不符);
因为该平面上的直线两两相交,也就是说不会出现平行的情况,在画出6条直线时,直线旋转过5次,5×30°=150°,如果再画出第7条直线,则旋转6次,6×30°=180°,这样第七条直线就与第一条直线平行了.
如图:

所以最多能画出六条.
(1)第2条至第6条直线与第1条直线 的“夹角”和是:30°+60°+90°+60°+30°=270°,
(2)第3条至第6条直线与第2条直线相交的“夹角”和是:270°-30°=240°,
(3)第4条至第6条直线与第3条直线相交的“夹角”和是:270°-30°-60°=180°,
(4)第5和第6条直线与第4条直线相交的“夹角”和是60°+30°=90°,
(5)第6条直线与第5条直线相交的“夹角”和是:30°
则270°+240°+180°+90°+60°=840°.
答:平面上最多有6条直线.当直线条数最多时,所有的“夹角”的和是840°.
因为该平面上的直线两两相交,也就是说不会出现平行的情况,在画出6条直线时,直线旋转过5次,5×30°=150°,如果再画出第7条直线,则旋转6次,6×30°=180°,这样第七条直线就与第一条直线平行了.
如图:

所以最多能画出六条.
(1)第2条至第6条直线与第1条直线 的“夹角”和是:30°+60°+90°+60°+30°=270°,
(2)第3条至第6条直线与第2条直线相交的“夹角”和是:270°-30°=240°,
(3)第4条至第6条直线与第3条直线相交的“夹角”和是:270°-30°-60°=180°,
(4)第5和第6条直线与第4条直线相交的“夹角”和是60°+30°=90°,
(5)第6条直线与第5条直线相交的“夹角”和是:30°
则270°+240°+180°+90°+60°=840°.
答:平面上最多有6条直线.当直线条数最多时,所有的“夹角”的和是840°.
点评:本题考查了对顶角、邻补角.根据题意,由题目给出的条件,通过旋转的方法进一步解答即可.

练习册系列答案
相关题目
将一次函数图象y=2x向右平移1个单位,所得图象对应的函数关系式为( )
| A、y=2x-2 |
| B、y=2x-1 |
| C、y=2x+1 |
| D、y=2x+2 |
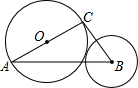 已知,如图,△ABC中,∠C=90,AC=12,BC=8,AC为⊙O的直径,⊙B的半径长为4.求证:⊙O与⊙B外切.
已知,如图,△ABC中,∠C=90,AC=12,BC=8,AC为⊙O的直径,⊙B的半径长为4.求证:⊙O与⊙B外切. 如图,点C为线段AB上一点,D为AC的中点,点E为线段BD的中点.
如图,点C为线段AB上一点,D为AC的中点,点E为线段BD的中点.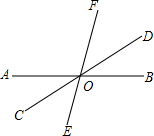 如图,已知直线AB,CD,EF相交于点O,∠COE:∠BOE=2:7,∠BOD=30°,求∠BOF的度数.
如图,已知直线AB,CD,EF相交于点O,∠COE:∠BOE=2:7,∠BOD=30°,求∠BOF的度数.