题目内容
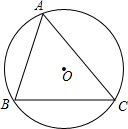 如图,圆O是锐角△ABC的外接圆,其半径为R.BC=a,AC=b,AB=c.求证:
如图,圆O是锐角△ABC的外接圆,其半径为R.BC=a,AC=b,AB=c.求证:| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
考点:正弦定理与余弦定理
专题:
分析:分别连接AO、BO、CO并交圆O于点D、E、F,连接BD、AF、EC,根据圆周角定理可得:∠A=∠BEC,∠B=∠AFC,∠C=∠ADB,然后分别在△BEC、△AFC、△ABD中,求出sinA、sinB、sinC的值,继而可求证.
解答:解: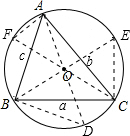 连接AO、BO、CO并交圆O于点D、E、F,连接BD、AF、EC,
连接AO、BO、CO并交圆O于点D、E、F,连接BD、AF、EC,
由圆周角定理可得:∠A=∠BEC,∠B=∠AFC,∠C=∠ADB,
则在△BEC中,
sin∠BEC=
=
,
∵∠A=∠BEC,
∴sinA=
,即
=2R,
同理可证:sinB=sin∠AFC=
,sinC=sin∠ADB=
,
即
=2R,
=2R,
∴
=
=
=2R.
 连接AO、BO、CO并交圆O于点D、E、F,连接BD、AF、EC,
连接AO、BO、CO并交圆O于点D、E、F,连接BD、AF、EC,由圆周角定理可得:∠A=∠BEC,∠B=∠AFC,∠C=∠ADB,
则在△BEC中,
sin∠BEC=
| BC |
| BE |
| a |
| 2R |
∵∠A=∠BEC,
∴sinA=
| a |
| 2R |
| a |
| sinA |
同理可证:sinB=sin∠AFC=
| b |
| 2R |
| c |
| 2R |
即
| b |
| sinB |
| c |
| sinC |
∴
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
点评:本题考查了正弦定理和余弦定理,解答本题的关键是作辅助线构造直角三角形,利用三角函数的知识进行解答,难度适中.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
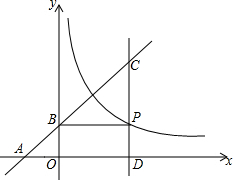 如图,直线y=x+m分别交坐标轴于A、B两点,且交平行于y轴的直线CD:x=n于点C;过点B作BP⊥CD,垂足为P.已知△OAB与△BPC的面积和为30,四边形OBPD的周长为20.若点P为反比例函数y=
如图,直线y=x+m分别交坐标轴于A、B两点,且交平行于y轴的直线CD:x=n于点C;过点B作BP⊥CD,垂足为P.已知△OAB与△BPC的面积和为30,四边形OBPD的周长为20.若点P为反比例函数y=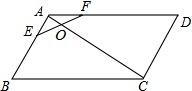 如图,平行四边形ABCD中,E、F分别是边AB、AD上的点,EF交AC于点O,且AE:EB=1:2,AO=3,FO=2,EO=4,则AC=
如图,平行四边形ABCD中,E、F分别是边AB、AD上的点,EF交AC于点O,且AE:EB=1:2,AO=3,FO=2,EO=4,则AC= 如图,∠1与∠B是直线
如图,∠1与∠B是直线 如图,请你数出五角星中同旁内角的对数.
如图,请你数出五角星中同旁内角的对数.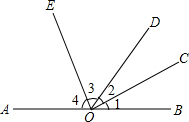 如图,O为直线AB上一点,OC平分∠BOD,EO⊥OC,垂足为点O,试判断∠3与∠4的关系.
如图,O为直线AB上一点,OC平分∠BOD,EO⊥OC,垂足为点O,试判断∠3与∠4的关系.