题目内容
4.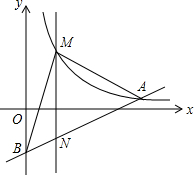 如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(a>0)的图象经过点A,动直线x=t,(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(a>0)的图象经过点A,动直线x=t,(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.(1)求k的值;
(2)求△BMN面积的最大值.
分析 (1)把点A坐标代入y=$\frac{k}{x}$(x>0),即可求出k的值;
(2)先求出直线AB的解析式,利用t表示出M和N的纵坐标,则△MNB的面积即可利用t表示,即△BMN的面积是t的二次函数,即可得出面积的最大值.
解答 解:(1)把点A(8,1)代入反比例函数y=$\frac{k}{x}$(x>0)得:
k=1×8=8,y=$\frac{8}{x}$,
∴k=8;
(2)设直线AB的解析式为:y=kx+b,
根据题意得:$\left\{\begin{array}{l}{8k+b=1}\\{b=-3}\end{array}\right.$,
解得:k=$\frac{1}{2}$,b=-3,
∴直线AB的解析式为:y=$\frac{1}{2}$x-3;
设M(t,$\frac{8}{t}$),N(t,$\frac{1}{2}$t-3),
则MN=$\frac{8}{t}$-$\frac{1}{2}$t+3,
∴△BMN的面积S=$\frac{1}{2}$($\frac{8}{t}$-$\frac{1}{2}$t+3)t=-$\frac{1}{4}$t2+$\frac{3}{2}$t+4=-$\frac{1}{4}$(t-3)2+$\frac{25}{4}$,
∴△BMN的面积S是t的二次函数,
∵-$\frac{1}{4}$<0,
∴S有最大值,
当t=3时,△BMN的面积的最大值为$\frac{25}{4}$.
点评 本题是反比例函数一次函数和二次函数的综合应用,正确利用t表示出三角形MNB的面积是关键.

练习册系列答案
相关题目
15.点P(-2013,2014)在平面直角坐标系中所在的位置是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.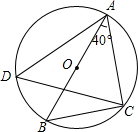 如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
 如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
9.某校七年级全体学生到电影院观看影片.设电影院的座位有x排,若每排坐18人,则有32人无座位;若每排坐20人,则只有8个座位无人坐.下列方程中正确的是( )
| A. | 18x+32=20x-8 | B. | 18x+32=20x+8 | C. | 18x-32=20x-8 | D. | 18x-32=20x+8 |
16.下列各数中,无理数的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{25}$ | C. | $\frac{7}{13}$ | D. | 3.1415 |
 A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.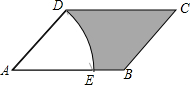 如图,在平行四边形ABCD中,∠A=45°,以A为圆心,AD为半径画弧交AB于E,AD=2,EB=1,则图中阴影部分的面积是3$\sqrt{2}$-$\frac{1}{2}$π(保留π).
如图,在平行四边形ABCD中,∠A=45°,以A为圆心,AD为半径画弧交AB于E,AD=2,EB=1,则图中阴影部分的面积是3$\sqrt{2}$-$\frac{1}{2}$π(保留π).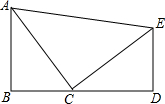 如图,AB⊥BD,ED⊥BD于D,AB=CD,AC=CE,下列结论:(1)BC=DE;(2)AC⊥CE;(3)∠CAE=45°,其中正确的有( )
如图,AB⊥BD,ED⊥BD于D,AB=CD,AC=CE,下列结论:(1)BC=DE;(2)AC⊥CE;(3)∠CAE=45°,其中正确的有( )