Question

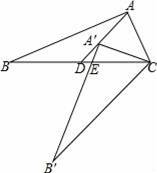
如图，Rt△ABC中，∠BAC=90°，将△ABC绕点C逆时针旋转，旋转后的图形是△A′B′C，点A的对应点A′落在中线AD上，且点A′是△ABC的重心，A′B′与BC相交于点E，那么BE：CE=　　　　　　．

　

Answer 1

4：3　．

【考点】旋转的性质；三角形的重心．

【专题】计算题；平移、旋转与对称．

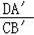
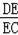
【分析】先证明DA′=CB′，由DA′∥CB′，得==即可解决问题．

【解答】证明：∵∠BAC=90°，A′是△ABC重心，

∴BD=DC=AD，DA′=AA′=AD=BC，

∵△A′CB′S是由△ABC旋转得到，

∴CA′=CA，BC=CB′，∠ACB=∠A′CB′=∠DAC，∠CA′B′=90°，

∴∠CAA′=∠CA′A=∠DAC，∠DA′B′+′CA′A=90°，∠B′+∠A′CB′=90°，

∴∠DA′B′=∠B′

∴DA′∥CB′，

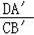
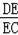
∴==，设DE=k，则EC=6k，BE=DC=7k，BE=8k，

∴BE：CE=8k：6k=4：3．

故答案为4：3．

【点评】本题考查三角形重心、旋转平行线分线段成比例定理等知识，解题的关键是发现DA′=CB′，记住三角形的重心把中线分成1：2两部分，属于中考常考题型．