题目内容
7. 如图,在△ABC中,两条中线BE,CD相交于点O,则OD:OC=$\frac{1}{2}$.
如图,在△ABC中,两条中线BE,CD相交于点O,则OD:OC=$\frac{1}{2}$.
分析 根据三角形的中位线得出DE∥BC,DE=$\frac{1}{2}$BC,根据平行线的性质得出相似,根据相似三角形的性质求出即可.
解答 解:∵BE和CD是△ABC的中线,
∴DE=$\frac{1}{2}$BC,DE∥BC,
∴$\frac{DE}{BC}=\frac{1}{2}$,△DOE∽△COB,
∴OD:OC=DE:BC=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了相似三角形的性质和判定,三角形的中位线的应用,注意:相似三角形的面积比等于相似比的平方,三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
12.将一个矩形纸片(厚度不计)置于太阳光下,改变纸片的摆放位置和方向,则其留在地面上的影子的形状一定不是( )
| A. | 三角形 | B. | 平行四边形 | C. | 矩形 | D. | 正方形 |
19.下列几何体中,主视图是三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.下列几何体中,主视图相同的是( )


| A. | ①② | B. | ①④ | C. | ①③ | D. | ②④ |
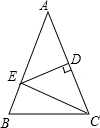 已知△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,D为垂足,连接EC.
已知△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,D为垂足,连接EC. 如图,若正三棱柱看不见的一个侧面与投影面平行,则这个正三棱柱的正投影是( )
如图,若正三棱柱看不见的一个侧面与投影面平行,则这个正三棱柱的正投影是( )



 如图,边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角).
如图,边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角).