题目内容
4.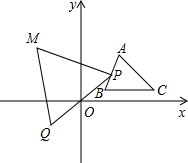 如图,△ABC在第一象限,其面积为8.点P从点A出发,沿△ABC的边从A-B-C-A运动一周,在点P运动的同时,作点P关于原点O的对称点Q,再以PQ为边作等边三角形PQM,点M在第二象限,点M随点P运动所形成的图形的面积为24.
如图,△ABC在第一象限,其面积为8.点P从点A出发,沿△ABC的边从A-B-C-A运动一周,在点P运动的同时,作点P关于原点O的对称点Q,再以PQ为边作等边三角形PQM,点M在第二象限,点M随点P运动所形成的图形的面积为24.
分析 设M点对应的A,B,C的点分别为Ma,Mb,Mc,由△MbQbB是等边三角形,得出MbO=$\sqrt{3}$OB,同理McO=$\sqrt{3}$OC,又因∠COB=∠McOMb,得出△McOMb∽△COB,得出MbMc=$\sqrt{3}$BC,同理,MaMb=$\sqrt{3}$AB,MaMc=$\sqrt{3}$AC,所以△MaMbMc的面积是△ABC的3倍.求出点M随点P运动所形成的图形的面积为24.
解答 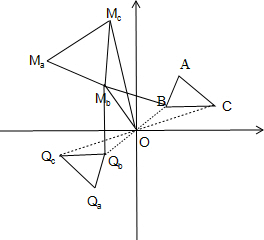 解:如图,∵点P从点A出发,沿△ABC的边从A-B-C-A运动一周,且点Q关于原点O与点P对称,
解:如图,∵点P从点A出发,沿△ABC的边从A-B-C-A运动一周,且点Q关于原点O与点P对称,
∴点Q随点P运动所形成的图形是△ABC关于O的中心对称图形,
以PQ为边作等边△PQM,M点对应的A,B,C的点分别为Ma,Mb,Mc,
∵△MbQbB是等边三角形,
∴MbO=$\sqrt{3}$OB,
同理McO=$\sqrt{3}$OC,
∴$\frac{{M}_{b}O}{BO}$=$\frac{{M}_{c}O}{CO}$=$\sqrt{3}$,
∵∠COB+∠BOMc=90°,∠McOMb+∠BOMc=90°
∴∠COB=∠McOMb,
∴△McOMb∽△COB,
∴MbMc=$\sqrt{3}$BC,
同理,MaMb=$\sqrt{3}$AB,MaMc=$\sqrt{3}$AC,
∴△MaMbMc的面积=$\sqrt{3}$×$\sqrt{3}$×8=24,
即点M随点P运动所形成的图形的面积为24.
故答案为:24.
点评 本题主要考查了轨迹,轴对称的性质以及等边三角形的性质,解题的关键是找出△MaMbMc与△ABC边长的关系.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
16.已知O半径为3,A为线段PO的中点,则当OP=7时,点A与O的位置关系为( )
| A. | 点在圆内 | B. | 点在圆上 | C. | 点在圆外 | D. | 不能确定 |
13.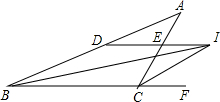 如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
 如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )| A. | 2cm | B. | 5cm | C. | 4cm | D. | 5cm |
14.一个多边形的每个外角都是45°,那么这个多边形的内角和等于( )
| A. | 720° | B. | 900° | C. | 675° | D. | 1080° |
 如图所示,求阴影部分的面积.
如图所示,求阴影部分的面积.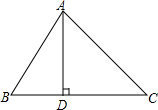 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.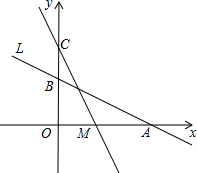 如图,直线L:y=-$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
如图,直线L:y=-$\frac{1}{2}$x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.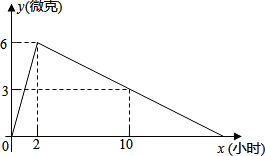 某医药研究所研发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达每毫升6微克,接着逐步衰减,服药后10小时血液中含药量为3微克,含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后.
某医药研究所研发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达每毫升6微克,接着逐步衰减,服药后10小时血液中含药量为3微克,含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后.