题目内容
9.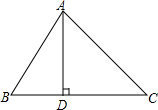 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.(1)求∠BAC的度数.
(2)若AD=2,求AC的长.
分析 (1)直接根据三角形内角和定理即可求出∠BAC的度数;
(2)先根据∠C=45°判断出△ADC的形状,再由勾股定理即可得出结论.
解答 解:(1)∵在△ABC中,∠B=60°,∠C=45°,
∴∠BAC=180°-60°-45°=75°;
(2)∵AD⊥BC,
∴△ADC是直角三角形,
又∵∠C=45°,
∴AD=DC,
∴根据勾股定理,得2AD2=AC2,即AC=2$\sqrt{2}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
 设函数y=-x2+2(m-1)x+m+1的图象如图所示,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为2.
设函数y=-x2+2(m-1)x+m+1的图象如图所示,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为2.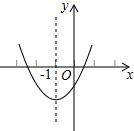 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc<0;②2a+b=0;③a+b+c>0;④b2>4ac.其中正确的有①③④.
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc<0;②2a+b=0;③a+b+c>0;④b2>4ac.其中正确的有①③④.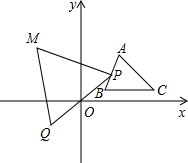 如图,△ABC在第一象限,其面积为8.点P从点A出发,沿△ABC的边从A-B-C-A运动一周,在点P运动的同时,作点P关于原点O的对称点Q,再以PQ为边作等边三角形PQM,点M在第二象限,点M随点P运动所形成的图形的面积为24.
如图,△ABC在第一象限,其面积为8.点P从点A出发,沿△ABC的边从A-B-C-A运动一周,在点P运动的同时,作点P关于原点O的对称点Q,再以PQ为边作等边三角形PQM,点M在第二象限,点M随点P运动所形成的图形的面积为24.