��Ŀ����
9��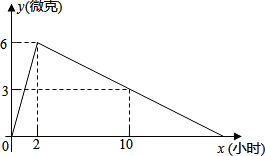 ijҽҩ�о����з���һ����ҩ��������ҩЧʱ���֣�������˰��涨�������ã���ô��ҩ��2СʱѪҺ�к�ҩ����ߣ���ÿ����6�ˣ�������˥������ҩ��10СʱѪҺ�к�ҩ��Ϊ3�ˣ���ҩ��y���ˣ���ʱ��x��Сʱ���ı仯��ͼ��ʾ�������˰��涨������ҩ��
ijҽҩ�о����з���һ����ҩ��������ҩЧʱ���֣�������˰��涨�������ã���ô��ҩ��2СʱѪҺ�к�ҩ����ߣ���ÿ����6�ˣ�������˥������ҩ��10СʱѪҺ�к�ҩ��Ϊ3�ˣ���ҩ��y���ˣ���ʱ��x��Сʱ���ı仯��ͼ��ʾ�������˰��涨������ҩ����1���ֱ����0��x��2��x��2ʱ��y��x�ĺ�����ϵʽ��
��2�����ÿ����ѪҺ�к�ҩ��Ϊ4�˻�4������ʱ��������ʱ����Ч�ģ���ô�����Чʱ���Ƕ��
���� ��1��ֱ�Ӹ���ͼ���ϵĵ���������ô���ϵ������⼴����ô𰸣�ע�0��x��2ʱ��y��x����������������x��2ʱy��x��һ�κ�����ϵ��
��2������ͼ���֪ÿ����ѪҺ�к�ҩ��Ϊ4��������������ͼ���϶��У�����y=4������y=3x����ÿ�ʼ����Ч���õ�ʱ�䣬��ͼ���֪˥��������y=4ʱ��ʱ�䣬��������ô𰸣�
��� �⣺��1����0��x��2ʱ����y=kx��
�ѣ�2��6��������ʽ����k=3��
��x0��x��2ʱ��y=3x��
��x��2ʱ����y=kx+b��
�ѣ�2��6������10��3��������ʽ��
�ã�$\left\{\begin{array}{l}{2k+b=6}\\{10k+b=3}\end{array}\right.$��
��ã�k=-$\frac{3}{8}$��b=$\frac{27}{4}$��
��x��2ʱ��y=-$\frac{3}{8}$x+$\frac{27}{4}$��
��2����y=4����y=3x���ɵ�x=$\frac{4}{3}$��
��y=4����y=-$\frac{3}{8}$x+$\frac{27}{4}$��
��ã�x=$\frac{22}{3}$��
��$\frac{22}{3}$-$\frac{4}{3}$=6��
�������Чʱ����6Сʱ��
���� ��Ҫ��������һ�κ�����ģ�ͽ��ʵ������������Ͷ�ͼ������Ҫ�ȸ��������г�������ϵʽ���ٴ�����ֵ������Ĺؼ���Ҫ�����������ʵ������ȷ���г�����ʽ���ٰѶ�Ӧֵ������⣬�������ͼʾ�ó�����Ҫ����Ϣ��

| A�� | $\frac{3}{8}$ | B�� | $\frac{3}{10}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{3}{4}$ |
| A�� | a��b����ͬ�� | B�� | a��b����Ҹ����ľ���ֵ�� | ||
| C�� | a��b����ͬ�� | D�� | a��b����������ľ���ֵ�� |
 ��ͼ����һ�����������߷ֱ�Ϊ50cm��40cm��30cm��ľ�䣬���ܷ��һ����Ϊ70cm��ľ���Ž�ȥ����˵��������ɣ�
��ͼ����һ�����������߷ֱ�Ϊ50cm��40cm��30cm��ľ�䣬���ܷ��һ����Ϊ70cm��ľ���Ž�ȥ����˵��������ɣ�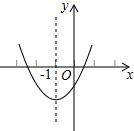 ��ͼΪ���κ���y=ax2+bx+c��a��0����ͼ��������˵������abc��0����2a+b=0����a+b+c��0����b2��4ac��������ȷ���Т٢ۢܣ�
��ͼΪ���κ���y=ax2+bx+c��a��0����ͼ��������˵������abc��0����2a+b=0����a+b+c��0����b2��4ac��������ȷ���Т٢ۢܣ�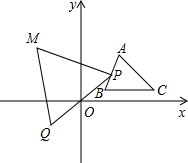 ��ͼ����ABC�ڵ�һ���ޣ������Ϊ8����P�ӵ�A�������ء�ABC�ıߴ�A-B-C-A�˶�һ�ܣ��ڵ�P�˶���ͬʱ������P����ԭ��O�ĶԳƵ�Q������PQΪ�����ȱ�������PQM����M�ڵڶ����ޣ���M���P�˶����γɵ�ͼ�ε����Ϊ24��
��ͼ����ABC�ڵ�һ���ޣ������Ϊ8����P�ӵ�A�������ء�ABC�ıߴ�A-B-C-A�˶�һ�ܣ��ڵ�P�˶���ͬʱ������P����ԭ��O�ĶԳƵ�Q������PQΪ�����ȱ�������PQM����M�ڵڶ����ޣ���M���P�˶����γɵ�ͼ�ε����Ϊ24��