题目内容
 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H(1)求∠APB度数;
(2)求证:△ABP≌△FBP;
(3)求证:AH+BD=AB.
考点:全等三角形的判定与性质
专题:
分析:(1)根据角平分线性质可得∠PAB+∠PBA=45°,即可解题;
(2)易得∠DPB=45°,可得∠BPF=135°,即可证明△ABP≌△FBP;
(3)由(2)结论可得∠F=∠BAD,AP=PF,AB=BF,即可求得∠F=∠CAD,即可证明△APH≌△FPD,可得AH=DF,即可解题.
(2)易得∠DPB=45°,可得∠BPF=135°,即可证明△ABP≌△FBP;
(3)由(2)结论可得∠F=∠BAD,AP=PF,AB=BF,即可求得∠F=∠CAD,即可证明△APH≌△FPD,可得AH=DF,即可解题.
解答:解:(1)∵AD平分∠BAC,BE平分∠ABC,
∴∠PAB+∠PBA=
(∠ABC+∠BAC)=45°,
∴∠APB=180°-45°=135°;
(2)∵∠APB=135°,
∴∠DPB=45°,
∵PF⊥AD,
∴∠BPF=135°,
在△ABP和△FBP中,
,
∴△ABP≌△FBP(ASA);
(3)∵△ABP≌△FBP,
∴∠F=∠BAD,AP=PF,AB=BF,
∵∠BAD=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
,
∴△APH≌△FPD(ASA),
∴AH=DF,
∵BF=DF+BD,
∴AB=AH+BD.
∴∠PAB+∠PBA=
| 1 |
| 2 |
∴∠APB=180°-45°=135°;
(2)∵∠APB=135°,
∴∠DPB=45°,
∵PF⊥AD,
∴∠BPF=135°,
在△ABP和△FBP中,
|
∴△ABP≌△FBP(ASA);
(3)∵△ABP≌△FBP,
∴∠F=∠BAD,AP=PF,AB=BF,
∵∠BAD=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
|
∴△APH≌△FPD(ASA),
∴AH=DF,
∵BF=DF+BD,
∴AB=AH+BD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABP≌△FBP和△APH≌△FPD是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地.两车同时出发,两车相遇时快车因机械小故障要将所有乘客转移到慢车上,转移乘客后慢车按原速改变方向立即驶向乙地.快车转移乘客后立即在原地用了2小时进行维修.然后按原速驶往乙地,结果两车同时到达终点,设行驶时间未x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行一下探究;
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地.两车同时出发,两车相遇时快车因机械小故障要将所有乘客转移到慢车上,转移乘客后慢车按原速改变方向立即驶向乙地.快车转移乘客后立即在原地用了2小时进行维修.然后按原速驶往乙地,结果两车同时到达终点,设行驶时间未x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行一下探究;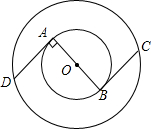 如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=
如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=