题目内容
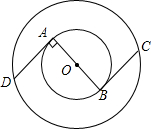 如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=
如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=| 2 |
(1)观察图形,下列关于这个图形的说法中,正确的是
A、只是中心对称图形 B、只是轴对称图形
C、既是中心对称图形又是轴对称图形 D、不是对称图形
(2)求图中环形(大圆内部与小圆外部的公共部分)的面积;
(3)请写出与AD有关的三个不同类型的正确结论(不需证明).
考点:切线的性质,圆与圆的位置关系
专题:
分析:(1)根据轴对称图形与中心对称图形的概念求解.
(2)连接OC,根据勾股定理求得R2-r2=2,然后根据S环形=S大圆-S小圆即可求得;
(3)根据平行线的性质,切线的判定,以及勾股定理即可得出结论;
(2)连接OC,根据勾股定理求得R2-r2=2,然后根据S环形=S大圆-S小圆即可求得;
(3)根据平行线的性质,切线的判定,以及勾股定理即可得出结论;
解答: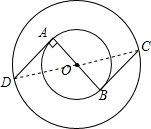 解:(1)由图形的对称性知图形是中心对称图形.
解:(1)由图形的对称性知图形是中心对称图形.
故选A;
(2)连接OC,
∵BC与小圆相切于点B,
∴OB⊥BC,
∴在RT△OBC中,OC2-OB2=BC2,
即R2-r2=(
)2=2,
∴S环形=S大圆-S小圆=πR2-πr2=π(R2-r2)=2π;
(3)AD=BC,AD⊥AB,AD是小圆的切线;
∵AD∥BC,AB⊥BC,
∴AD⊥AB,
∵AB是小圆的直径,
∴AD是小圆的切线;
∵AD2=R2-r2,BC2=R2-r2,
∴AD=BC;
 解:(1)由图形的对称性知图形是中心对称图形.
解:(1)由图形的对称性知图形是中心对称图形.故选A;
(2)连接OC,
∵BC与小圆相切于点B,
∴OB⊥BC,
∴在RT△OBC中,OC2-OB2=BC2,
即R2-r2=(
| 2 |
∴S环形=S大圆-S小圆=πR2-πr2=π(R2-r2)=2π;
(3)AD=BC,AD⊥AB,AD是小圆的切线;
∵AD∥BC,AB⊥BC,
∴AD⊥AB,
∵AB是小圆的直径,
∴AD是小圆的切线;
∵AD2=R2-r2,BC2=R2-r2,
∴AD=BC;
点评:本题考查了中心对称图形与轴对称图形的概念,圆环的面积的求法,切线的判定,以及勾股定理等,作出辅助线构建直角三角形是本题的关键;

练习册系列答案
相关题目
 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
 校门口经常有人搞摸奖.在一只黑色的口袋里装有处颜色外都相同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,任意摸1个球.奖品的情况标注在球上.
校门口经常有人搞摸奖.在一只黑色的口袋里装有处颜色外都相同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,任意摸1个球.奖品的情况标注在球上. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长. 如图,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=
如图,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y= 如图,∠AOB=90°,CD是
如图,∠AOB=90°,CD是