题目内容
5.已知抛物线的C1顶点为E(-1,4),与y轴交于C(0,3).(1)求抛物线C1的解析式;
(2)如图1,过顶点E作EF⊥x轴于F点,交直线AC于D,点P、Q分别在抛物线C1和x轴上,若Q为(t,0),且以E、D、P、Q为顶点的四边形为平行四边形,求t的值;
(3)如图2,将抛物线C1向右平移一个单位得到抛物线C2,直线y=kx+6与y轴交于点H,与抛物线C2交于M、N两个不同点,分别过M、N两点作y轴的垂线,垂足分别为P、Q,当k的值在取值范围内发生变化时,式子$\frac{1}{HP}$+$\frac{1}{HQ}$的值是否发生变化?若不变,请求其值.(解此题时不用相似知识)

分析 (1)运用顶点式待定系数法求解即可;
(2)根据点Q坐标,表示点P坐标,进一步表示PQ长度,由平行四边形的对边相等列出方程求解即可;
(3)联立直线和抛物线求出交点坐标,表示HP,HQ的长度,代入化简即可.
解答 解:(1)设抛物线C1的解析式为:y=a(x+1)2+4,把点C(0,3)的坐标代入得,a=1,
故抛物线C1的解析式为:y=-(x+1)2+4=-x2-2x+3;
(2)如图1,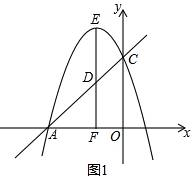
由题意得,PQ∥DE,
由点P(t,0),得点Q(t,-t2-2t+3),
所以有:PQ=|-t2-2t+3|,
y=-(x+1)2+4,令y=0,解得:x=-3,或x=1,
∴点A(-3,0),
运用两点法可求直线AC的解析式为:y=x+3,
当x=-1时,y=2,
∴点D(-1,2),
DE=4-2=2,
由平行四边形性质可得:PQ=DE,
|-t2-2t+3|=2,
解得:t=$-1±\sqrt{2}$,或t=-1$±\sqrt{6}$;
(3)如图2,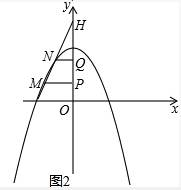
抛物线C1向右平移一个单位得到抛物线C2的解析式为:y=-x2+4,
联立方程组:$\left\{\begin{array}{l}{y=-{x}^{2}+4}\\{y=kx+6}\end{array}\right.$,
解得:x=$\frac{-k±\sqrt{{k}^{2}-8}}{2}$,y=$\frac{-{k}^{2}+12±k\sqrt{{k}^{2}-8}}{2}$,
∴HP=$\frac{{k}^{2}+k\sqrt{{k}^{2}-8}}{2}$,HQ=$\frac{{k}^{2}-k\sqrt{{k}^{2}-8}}{2}$,
HP+HQ=k2,HP×HQ=2k2,
∴$\frac{1}{HP}+\frac{1}{HQ}=\frac{HQ+HP}{HQ×HP}$=$\frac{1}{2}$.
点评 此题主要考查二次函数的综合问题,会用待定系数法求解析式,知道运用平行四边形的性质建立方程并准确求解,会求含有字母系数的方程组,并化简分式是解题的关键.

 如图是一种常用的圆顶螺杆,它的主视图是( )
如图是一种常用的圆顶螺杆,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 求图中x的值.
求图中x的值. 如图,DE+AB=AD,∠1=∠E.求证:
如图,DE+AB=AD,∠1=∠E.求证: 如图,在?ABCD中,E为BC上的一点,且AE与DE分别平分∠BAD和∠ADC
如图,在?ABCD中,E为BC上的一点,且AE与DE分别平分∠BAD和∠ADC 如图,AB是⊙O的直径,点C在半圆上从点A运动到点B(点C不与A、B重合),过点B作⊙O的切线,交AC的平行线OD于点D,连接CB交OD于点E.连接CD,已知:AB=10.
如图,AB是⊙O的直径,点C在半圆上从点A运动到点B(点C不与A、B重合),过点B作⊙O的切线,交AC的平行线OD于点D,连接CB交OD于点E.连接CD,已知:AB=10. 已知:如图,D是△ABC中BC边上一点,且AD⊥BC,E是AD上的一点,EB=EC,求证:∠BAE=∠CAE.
已知:如图,D是△ABC中BC边上一点,且AD⊥BC,E是AD上的一点,EB=EC,求证:∠BAE=∠CAE.