题目内容
方程(m2-1)x2-2(m+2)x+1=0的不同实根只有1个,则m= .
考点:根的判别式
专题:计算题
分析:根据方程(m2-1)x2-2(m+2)x+1=0的不同实根只有1个可得△=0,得到关于m的方程求得m的值即可;
解答:解:∵①方程(m2-1)x2-2(m+2)x+1=0的不同实根只有1个,
∴△=4(m+2)2-4(m2-1)=0
解得:m=-
,
②当m2-1=0时,方程为一元一次方程,
∴m=±1.
故答案为±1或-
.
∴△=4(m+2)2-4(m2-1)=0
解得:m=-
| 3 |
| 4 |
②当m2-1=0时,方程为一元一次方程,
∴m=±1.
故答案为±1或-
| 3 |
| 4 |
点评:本题考查了根的判别式的知识,解题的关键是分类讨论.

练习册系列答案
相关题目
从装有7种颜色每色77个球的袋中摸球出来,摸时没法判断颜色,要确保摸出的球装满7盒,每盒7个球,盒中的球同色,则至少需要摸出( )个球.
| A、85 | B、84 | C、71 | D、50 |
 如图,M是平行四边形ABCD中CD边上一点,也是△ABE中AE边上的点,且EM=2AM,则S□ABCD:S△ABE=( )
如图,M是平行四边形ABCD中CD边上一点,也是△ABE中AE边上的点,且EM=2AM,则S□ABCD:S△ABE=( )| A、3:2 | B、2:3 |
| C、2:1 | D、1:2 |
 如图,两个邻接的正方形的面积分别为4和196,那么,这两个正方形内切圆圆心距是( )
如图,两个邻接的正方形的面积分别为4和196,那么,这两个正方形内切圆圆心距是( )| A、10 | ||
B、8
| ||
C、10
| ||
| D、8 |
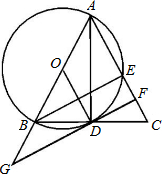 于F,交AB的延长线于G,连接AD.若AB:BG=3:1,FG⊥AC.
于F,交AB的延长线于G,连接AD.若AB:BG=3:1,FG⊥AC. 如图是一卷紧紧缠绕在一起的牛皮纸,纸卷直径为20厘米;中间有一直径为6厘米的卷轴.已知纸的厚度为0.4厘米.试求这卷纸展开后大约有多少厘米?
如图是一卷紧紧缠绕在一起的牛皮纸,纸卷直径为20厘米;中间有一直径为6厘米的卷轴.已知纸的厚度为0.4厘米.试求这卷纸展开后大约有多少厘米?