题目内容
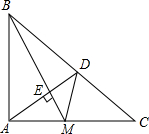 如图,设点M是等腰Rt△ABC的直角边AC的中点,AD⊥BM于E,AD交BC于D.求证:∠AMB=∠CMD(请用两种不同的方法证明)
如图,设点M是等腰Rt△ABC的直角边AC的中点,AD⊥BM于E,AD交BC于D.求证:∠AMB=∠CMD(请用两种不同的方法证明)考点:等腰直角三角形,三角形内角和定理,相似三角形的判定与性质
专题:
分析:法(1)先延长AD至F,使得CF⊥AC,得出∠ABM=∠DAC,再根据AB=AC,CF⊥AC,得出△ABM≌△CAF,从而证出∠BMA=∠F,AM=CF,再根据所给的条件得出△FCD≌△MCD,即可得出∠AMB=∠F=∠CMD;
法(2)先作∠BAC的平分线交BM于N,得出∠ABN=∠CAE,再根据∠BAN=∠C=45°,AB=AC,证出△BAN≌△ACD,得出AN=CD,证出△NAM≌△DCM,即可得出∠AMB=∠CMD.
法(2)先作∠BAC的平分线交BM于N,得出∠ABN=∠CAE,再根据∠BAN=∠C=45°,AB=AC,证出△BAN≌△ACD,得出AN=CD,证出△NAM≌△DCM,即可得出∠AMB=∠CMD.
解答:证明:法(1)如图,延长AD至F,使得CF⊥AC,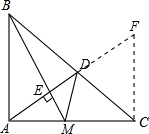
∵AB⊥AC,AD⊥BM,
∴∠ABM=∠DAC,
又∵AB=AC,CF⊥AC,
∴△ABM≌△CAF,
∴∠BMA=∠F,AM=CF,
∵∠BCA=∠BCF=45°,AM=CM=CF,DC=DC,
∴△FCD≌△MCD,
∴∠AMB=∠F=∠CMD;
法(2)AD交BM于E,作∠BAC的平分线交BM于N,
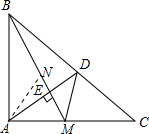
∵AE⊥BM,BA⊥AC,
∴∠ABN=∠CAE,
∵∠BAN=∠C=45°,AB=AC,
∴△BAN≌△ACD.
∴AN=CD,
∵∠NAM=∠C=45°,AM=MC
∴△NAM≌△DCM,
∴∠AMB=∠CMD.

∵AB⊥AC,AD⊥BM,
∴∠ABM=∠DAC,
又∵AB=AC,CF⊥AC,
∴△ABM≌△CAF,
∴∠BMA=∠F,AM=CF,
∵∠BCA=∠BCF=45°,AM=CM=CF,DC=DC,
∴△FCD≌△MCD,
∴∠AMB=∠F=∠CMD;
法(2)AD交BM于E,作∠BAC的平分线交BM于N,

∵AE⊥BM,BA⊥AC,
∴∠ABN=∠CAE,
∵∠BAN=∠C=45°,AB=AC,
∴△BAN≌△ACD.
∴AN=CD,
∵∠NAM=∠C=45°,AM=MC
∴△NAM≌△DCM,
∴∠AMB=∠CMD.
点评:此题考查了解等腰直角三角形;解题的关键是根据题意画出图形,再根据解等腰直角三角形的性质和相似三角形的判断与性质进行解答即可.

练习册系列答案
相关题目
如果
+
>2,那么有可能的是( )
| 1 |
| m |
| 1 |
| n |
| A、m>1,n>1 |
| B、m<0,n<0 |
| C、m>1,n>0 |
| D、m<0,n>1 |
从装有7种颜色每色77个球的袋中摸球出来,摸时没法判断颜色,要确保摸出的球装满7盒,每盒7个球,盒中的球同色,则至少需要摸出( )个球.
| A、85 | B、84 | C、71 | D、50 |
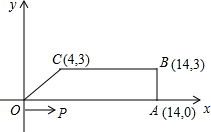 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为A(14,0)、B(14,3)、C(4,3),点P、Q为两动点,同时从原点出发,分别作匀速运动,其中P点沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,速度为每秒2个单位.且当这两点中有一点到达自己的终点时,另一点也停止运动.设运动的时间为t秒.
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为A(14,0)、B(14,3)、C(4,3),点P、Q为两动点,同时从原点出发,分别作匀速运动,其中P点沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,速度为每秒2个单位.且当这两点中有一点到达自己的终点时,另一点也停止运动.设运动的时间为t秒.
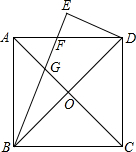 如图,正方形ABCD的对角线AC、BD交于点O,∠ABD的平分线BE交AC于G,交AD于F,且DE⊥BE.
如图,正方形ABCD的对角线AC、BD交于点O,∠ABD的平分线BE交AC于G,交AD于F,且DE⊥BE.