题目内容
18．
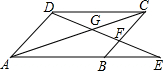如图，AC是平行四边形ABCD的对角线，DE与AB的延长线交于点E，与BC交于点F，与AC交于点G，则图中有相似三角形（ ）| A． | 3对 | B． | 4对 | C． | 5对 | D． | 6对 |
分析 根据平行四边形的性质得到：AD∥BC，AB∥CD，结合相似三角形的判定定理得到图中相似三角形．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，∠DAC=∠BCA，∠DCA=∠BAC，
∴△ADC∽△CBA，△ADG∽△CFG，△EFB∽△EDA，△DGC∽△EGA，△DFC～△EFB，共5对．
故选：C．
点评 本题考查了相似三角形的判定和平行四边形的性质．
平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；这是判定三角形相似的一种基本方法．相似的基本图形可分别记为“A”型和“X”型，如图所示在应用时要善于从复杂的图形中抽象出这些基本图形．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
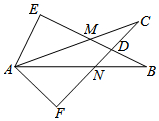如图所示，∠E=∠F=90°，∠B=∠C，AE=AF，有以下结论：①EM=FN；②CD=DN；③∠FAN=∠EAM；④△ACN≌△ABM．其中正确的结论有3个．
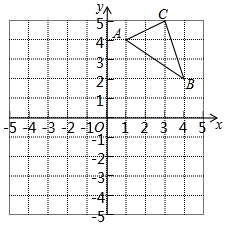如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．
如图，是用棋子摆成的图形，按照这种摆法，第n个图形中所需棋子的总数是用了n（n+1）个．
8．平面直角坐标系中，点P（m，n）在y轴上，且位于x轴的上方，下列结论中正确的是（ ）
| A． | m=0，n为任何实数 | B． | m=0，n＞0 | C． | m为任何实数，n=0 | D． | m＞0，n=0 |