题目内容
13．
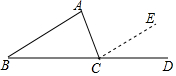如图，在证明“△ABC内角和等于180°”时，延长BC至D，过点C作CE∥AB，得到∠ABC=∠ECD，∠BAC=∠ACE，由于∠BCD=180°，可得到∠ABC+∠ACB+∠BAC=180°，这个证明方法体现的数学思想是（ ）| A． | 数形结合 | B． | 特殊到一般 | C． | 一般到特殊 | D． | 转化 |
分析 根据三角形内角和定理的证明过程，可寻找到转化的解题思想，此题得解．
解答 证明：∵∠ABC=∠ECD，∠BAC=∠ACE，∠BCD=∠BCA+∠ACE+∠ECD=180°，
∴∠BCA+∠BAC+∠ABC=180°．
此方法中用到了替换，体现了转化的思想．
故选D．
点评 本题考查了三角形内角和定理以及平行线的性质，根据证明过程找出转化思想是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．用反证法证明命题：在一个三角形中，最大的内角不小于60°，证明的第一步是（ ）
| A． | 假设最大的内角小于60° | B． | 假设最大的内角大于60° | ||
| C． | 假设最大的内角大等于60° | D． | 假设最大的内角小等于60° |
1．下面4个选项中，不是正方体的展开图的是（ ）
| A． |  | B． |  | C． |  | D． |  |
8．以x为未知数的方程$\frac{s}{x}$=$\frac{s+40}{x+v}$（s＞0，v＞0）的解为（ ）
| A． | x=$\frac{sv}{40}$ | B． | x=$\frac{sv}{50}$ | C． | x=$\frac{s+v}{40}$ | D． | x=$\frac{s-v}{40}$ |
18．下列图形既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，正方形ABCD的边长为6，点E为BC的中点，点F在AB边上，BF=2AF，H在BC延长线上，且CH=AF，连接DF，DE，DH．