题目内容
5. 如图,正方形ABCD的边长为6,点E为BC的中点,点F在AB边上,BF=2AF,H在BC延长线上,且CH=AF,连接DF,DE,DH.
如图,正方形ABCD的边长为6,点E为BC的中点,点F在AB边上,BF=2AF,H在BC延长线上,且CH=AF,连接DF,DE,DH.(1)求证DF=DH;
(2)求∠EDF的度数并写出计算过程.
分析 (1)根据正方形的性质和全等三角形的判定和性质证明即可.
(2)利用勾股定理得出Rt△DFG和Rt△EFG中,有FG2=DF2-DG2=EF2-EG2,求得DG=DF,进而解答即可.
解答 (1)证明∵正方形ABCD的边长为6,
∴AB=BC=CD=AD=6,∠A=∠B=∠ADC=∠DCE=90°.
∴∠DCH=180°-∠DCE=90°,∠A=∠DCH.
在△ADF和△CDH中,$\left\{\begin{array}{l}AD=CD\\∠A=∠DCH\\ AF=CH\end{array}\right.$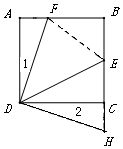
∴△ADF≌△CDH.(SAS)
∴DF=DH,
(2)连接EF,
∵△ADF≌△CDH
∴∠1=∠2.
∴∠FDH=∠FDC+∠2=∠FDC+∠1=∠ADC=90°.
∵点E为BC的中点,
∴BE=CE=3.
∵点F在AB边上,BF=2AF,
∴CH=AF=2,BF=4.
∴EH=CE+CH=5.
在Rt△BEF中,∠B=90°,$EF=\sqrt{B{E^2}+B{F^2}}=\sqrt{{3^2}+{4^2}}=5$.
∴$\underline{EF=EH}$.②
又∵DF=DH,①
DE=DE,③
由①②③得△DEF≌△DEH.(SSS)
∴$∠EDF=∠EDH=\frac{∠FDH}{2}=45°$.
点评 此题考查全等三角形的判定与性质,正方形的性质,等腰直角三角形的性质,以及勾股定理,利用了转化的数学思想方法.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
13.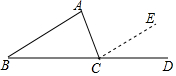 如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
 如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )| A. | 数形结合 | B. | 特殊到一般 | C. | 一般到特殊 | D. | 转化 |
15.2016年12月16日央视新闻报道:“不施肥不打药,袁隆平用海水种出红色水稻-海稻86”.其科研组在研究过程中,将“海稻86”在不同条件的甲、乙两块试验田进行试验,得到每块试验田每亩产量的两组数据,其方差分别为s2甲=0.002,s2乙=0.03,则( )
| A. | 甲比乙的产量稳定 | B. | 乙比甲的产量稳定 | ||
| C. | 甲、乙的产量一样稳定 | D. | 无法确定哪一品种的产量更稳定 |
 如图,是一个高速公路的隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面
如图,是一个高速公路的隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面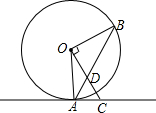 如图,点A,B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.求证:AC=CD.
如图,点A,B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.求证:AC=CD.