题目内容
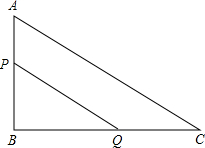 如图,在△ABC中,∠B=90°,AB=20cm,BC=30cm,动点P从A开始沿AB向B以2cm/s的速度移动;动点Q从点B开始沿BC向C以4cm/s的速度移动.若P、Q同时分别向A、B出发,那么△PBQ的面积S随时间t如何变化?写出S关于t的函数解析式及t的取值范围,并画出此函数图象.
如图,在△ABC中,∠B=90°,AB=20cm,BC=30cm,动点P从A开始沿AB向B以2cm/s的速度移动;动点Q从点B开始沿BC向C以4cm/s的速度移动.若P、Q同时分别向A、B出发,那么△PBQ的面积S随时间t如何变化?写出S关于t的函数解析式及t的取值范围,并画出此函数图象.考点:动点问题的函数图象
专题:
分析:根据三角形的面积公式列出函数式.t的取值范围由“时间=路程÷速度”得到.由函数解析式画出图象.
解答:解:依题意,得
S=
×4t•(20-2t)
=-4t2+40t
=-4(t-5)2+100(0<t≤7.5s).
即S=-4(t-5)2+100(0<t≤7.5s).
则该函数图象是抛物线,开口方向向下,顶点坐标是(5,100),且经过坐标原点(0,0).其图象如图所示:
.
由图象知,在0<t≤5时,S随t的增大而增大;当5<t≤7.5时,S随t的增大而减小.
S=
| 1 |
| 2 |
=-4t2+40t
=-4(t-5)2+100(0<t≤7.5s).
即S=-4(t-5)2+100(0<t≤7.5s).
则该函数图象是抛物线,开口方向向下,顶点坐标是(5,100),且经过坐标原点(0,0).其图象如图所示:
.

由图象知,在0<t≤5时,S随t的增大而增大;当5<t≤7.5时,S随t的增大而减小.
点评:本题考查了动点问题的函数图象.注意,在作函数图象时,由于t≠0,所以点O处要用空心点表示.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 已知四边形ABCD中,AD=a,CD=b,AB=AC=BC=c,求BD的最大值.
已知四边形ABCD中,AD=a,CD=b,AB=AC=BC=c,求BD的最大值. 如图,已知∠1=∠2,求证:DB+DC>AB+AC.
如图,已知∠1=∠2,求证:DB+DC>AB+AC. 如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方的B点.已知易拉罐底面周长是12cm,高是5cm,那么所需彩带最短是多少?
如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方的B点.已知易拉罐底面周长是12cm,高是5cm,那么所需彩带最短是多少? 如图,在梯形ABCD中,AD∥BC,AB=DC,梯形的周长为16cm,∠B=30°.设高AH为x(cm),中位线EF的长为y(cm),求y关于x的函数关系式,并求出自变量x的取值范围.
如图,在梯形ABCD中,AD∥BC,AB=DC,梯形的周长为16cm,∠B=30°.设高AH为x(cm),中位线EF的长为y(cm),求y关于x的函数关系式,并求出自变量x的取值范围.