题目内容
如图，已知∠1=∠2，求证：DB+DC＞AB+AC．考点：全等三角形的判定与性质,三角形三边关系
专题：证明题
分析：在BA的延长线上取AE=AC，连接DE，利用“边角边”证明△ADC和△ADE全等，根据全等三角形对应边相等可得DE=DC，再根据三角形的任意两边之和大于第三边证明即可．
解答：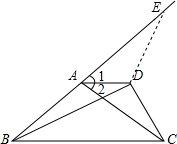
证明：如图，在BA的延长线上取AE=AC，连接DE，
在△ADC和△ADE中，
，
∴△ADC≌△ADE（SAS），
∴DE=DC，
在△BDE中，由三角形的三边关系得，DB+DE＞BE，
∴DB+DC＞AB+AC．
证明：如图，在BA的延长线上取AE=AC，连接DE，在△ADC和△ADE中，
|
∴△ADC≌△ADE（SAS），
∴DE=DC，
在△BDE中，由三角形的三边关系得，DB+DE＞BE，
∴DB+DC＞AB+AC．
点评：本题考查了全等三角形的判定与性质，三角形的三边关系，难点在于从∠1=∠2考虑作辅助线构造出全等三角形．
练习册系列答案
相关题目
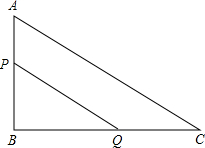如图，在△ABC中，∠B=90°，AB=20cm，BC=30cm，动点P从A开始沿AB向B以2cm/s的速度移动；动点Q从点B开始沿BC向C以4cm/s的速度移动．若P、Q同时分别向A、B出发，那么△PBQ的面积S随时间t如何变化？写出S关于t的函数解析式及t的取值范围，并画出此函数图象．
如图，两建筑物的水平距离BC是30m，从A点测得D点的俯角α是35°，测得C点的俯角β为43°，求这两座建筑物的高度．（结果保留整数）