题目内容
如图，小红想用一条彩带缠绕易拉罐，正好从A点绕到正上方的B点．已知易拉罐底面周长是12cm，高是5cm，那么所需彩带最短是多少？考点：平面展开-最短路径问题
专题：
分析：要求彩带的长，需将圆柱的侧面展开，进而根据“两点之间线段最短”得出结果，在求线段长时，借助于勾股定理．
解答：
解：由图可知，彩带从易拉罐底端的A处绕易拉罐4圈后到达顶端的B处，将易拉罐表面切开展开呈长方形，则螺旋线长为四个长方形并排后的长方形的对角线长，
∵易拉罐底面周长是12cm，高是5cm，
圆柱高6m，底面周长2m，
∴x2=（12×4）2+52=2304+25=2329，
所以彩带最短是
cm．
解：由图可知，彩带从易拉罐底端的A处绕易拉罐4圈后到达顶端的B处，将易拉罐表面切开展开呈长方形，则螺旋线长为四个长方形并排后的长方形的对角线长，∵易拉罐底面周长是12cm，高是5cm，
圆柱高6m，底面周长2m，
∴x2=（12×4）2+52=2304+25=2329，
所以彩带最短是
| 2329 |
点评：本题考查了平面展开-最短路径问题，圆柱的侧面展开图是一个矩形，此矩形的长等于圆柱底面周长，高等于圆柱的高，本题就是把圆柱的侧面展开成矩形，“化曲面为平面”，用勾股定理解决．
练习册系列答案
相关题目
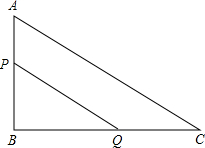如图，在△ABC中，∠B=90°，AB=20cm，BC=30cm，动点P从A开始沿AB向B以2cm/s的速度移动；动点Q从点B开始沿BC向C以4cm/s的速度移动．若P、Q同时分别向A、B出发，那么△PBQ的面积S随时间t如何变化？写出S关于t的函数解析式及t的取值范围，并画出此函数图象．
如图，两建筑物的水平距离BC是30m，从A点测得D点的俯角α是35°，测得C点的俯角β为43°，求这两座建筑物的高度．（结果保留整数）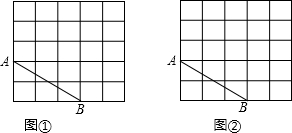
如图，在每个小正方形的边长均为1的方格纸中有一条线段AB，线段AB的两个端点均在小正方形的顶点上，请在图①、图②中各画一个三角形，它们的顶点均在小正方形的顶点上，且满足以下要求：