题目内容
若方程
-1=
有增根,则m的值是 .
| 6 |
| (x+1)(x-1) |
| m |
| (x-1)(x+2) |
考点:分式方程的增根
专题:
分析:增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x+1)(x-1)(x+2)=0,得到x=-1或1或-2,然后代入化为整式方程的方程算出m的值.
解答:解:方程两边都乘(x+1)(x-1)(x+2),
得6(x+2)-(x+1)(x-1)(x+2)=m(x+2)
∵原方程有增根,
∴最简公分母(x+1)(x-1)(x+2)=0,
解得x=-1或1或-2,
当x=-1时,m=6;
当x=1时,m=6,
当x=-2时,m无解.
故m的值是6.
故答案为:6.
得6(x+2)-(x+1)(x-1)(x+2)=m(x+2)
∵原方程有增根,
∴最简公分母(x+1)(x-1)(x+2)=0,
解得x=-1或1或-2,
当x=-1时,m=6;
当x=1时,m=6,
当x=-2时,m无解.
故m的值是6.
故答案为:6.
点评:本题考查了分式方程的增根.增根问题可按如下步骤进行:
①让最简公分母为0确定增根;
②化分式方程为整式方程;
③把增根代入整式方程即可求得相关字母的值.
①让最简公分母为0确定增根;
②化分式方程为整式方程;
③把增根代入整式方程即可求得相关字母的值.

练习册系列答案
相关题目
方程(
)x+(
)x=4的解x等于( )
2+
|
2-
|
| A、2 | B、-2 | C、2或-2 | D、无解 |
 如图,直线AD交⊙O于C,D两点,点B为圆上一点,BD平分∠ABO.若∠C=45°,∠BDA=60°,CD=
如图,直线AD交⊙O于C,D两点,点B为圆上一点,BD平分∠ABO.若∠C=45°,∠BDA=60°,CD=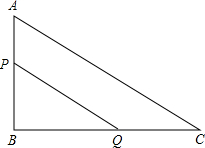 如图,在△ABC中,∠B=90°,AB=20cm,BC=30cm,动点P从A开始沿AB向B以2cm/s的速度移动;动点Q从点B开始沿BC向C以4cm/s的速度移动.若P、Q同时分别向A、B出发,那么△PBQ的面积S随时间t如何变化?写出S关于t的函数解析式及t的取值范围,并画出此函数图象.
如图,在△ABC中,∠B=90°,AB=20cm,BC=30cm,动点P从A开始沿AB向B以2cm/s的速度移动;动点Q从点B开始沿BC向C以4cm/s的速度移动.若P、Q同时分别向A、B出发,那么△PBQ的面积S随时间t如何变化?写出S关于t的函数解析式及t的取值范围,并画出此函数图象.