题目内容
11.(1)解方程:$\frac{2}{x-3}$-1=$\frac{1}{3-x}$(2)解不等式组:$\left\{\begin{array}{l}{2(x+2)<3x+3}\\{\frac{x+1}{4}>\frac{x}{3}}\end{array}\right.$.
分析 (1)根据分式方程的解法即可求出x的值.
(2)根据一元一次不等式组的解法即可求出答案.
解答 解:(1)$\frac{2}{x-3}-1=-\frac{1}{x-3}$
2-(x-3)=-1
2-x+3=-1
x=6
经检验:x=6时原分式方程的解
(2)由①可得:2x+4<3x+3
2x-3x<3-4
x>1
由②可得:3(x+1)>4x
3x+3>4x
x<3
∴不等式组的解集为:1<x<3
点评 本题考查学生的计算能力,解题的关键是熟练运用不等式的解法以及方程的解法,本题属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知点A的坐标是(a,b),若a+b<0,ab>0,则它在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
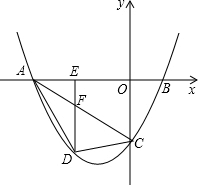 已知:如图,直线y=-$\frac{1}{2}$x-3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0).
已知:如图,直线y=-$\frac{1}{2}$x-3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0). 在A,B,C,D四幅图案中,能通过图案(1)平移得到的是( )
在A,B,C,D四幅图案中,能通过图案(1)平移得到的是( )



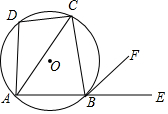 如图,四边形ABCD内接于⊙O,点E在AB的延长线上,BF∥AC,AB=BC,∠ADC=130°,则∠FBE=65°.
如图,四边形ABCD内接于⊙O,点E在AB的延长线上,BF∥AC,AB=BC,∠ADC=130°,则∠FBE=65°. 如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2=50度.
如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2=50度.