题目内容
在同一平面直角坐标系中画出一次函数y1=2x+2和二次函数y2=-
x2+
x+3的图象.
(1)求它们的交点坐标;
(2)当x为何值时,y1>y2?
| 1 |
| 2 |
| 3 |
| 2 |
(1)求它们的交点坐标;
(2)当x为何值时,y1>y2?
考点:二次函数的图象,一次函数的图象
专题:
分析:(1)首先画出两函数图象,进而求出两函数交点坐标;
(2)利用函数图象比较函数的大小关系.
(2)利用函数图象比较函数的大小关系.
解答: 解:(1)如图所示:
解:(1)如图所示:
,
解得:
,
.
故两函数交点坐标为:(1,4),(-2,-2);
(2)由图象可得:x>1或x<-2时,y1>y2.
 解:(1)如图所示:
解:(1)如图所示:
|
解得:
|
|
故两函数交点坐标为:(1,4),(-2,-2);
(2)由图象可得:x>1或x<-2时,y1>y2.
点评:此题主要考查了函数图象画法以及函数交点求法,利用数形结合得出函数大小关系是解题关键.

练习册系列答案
相关题目
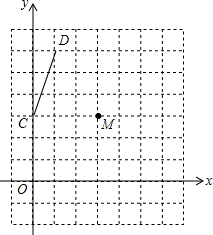 在平面直角坐标系中,已知点C(0,3)、D(1,6),将线段绕点M(3,3)旋转180°后,得到线段AB,则线段AB所在直线的函数解析式是 )
在平面直角坐标系中,已知点C(0,3)、D(1,6),将线段绕点M(3,3)旋转180°后,得到线段AB,则线段AB所在直线的函数解析式是 )| A、y=3x+15 |
| B、y=3x-15 |
| C、y=15x-3 |
| D、y=-15x+3 |
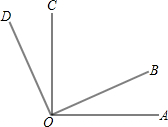 如图,已知∠AOC、∠BOD都是直角,∠AOC+∠AOD=211°,求∠AOB与∠BOC的度数.
如图,已知∠AOC、∠BOD都是直角,∠AOC+∠AOD=211°,求∠AOB与∠BOC的度数.