题目内容
如图1,已知双曲线y1=
(k>0)与直线y2=k'x交于A,B两点,点A在第一象限.试解答下列问题:

(1)若点A的坐标为(4,2),则点B的坐标为 ; 当x满足 时,y1>y2;当y1<2时,x的取值范围为 ;当x>-4时,y2的取值范围为 .
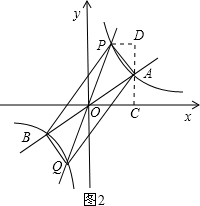
(2)过原点O作另一条直线l,交双曲线y=
(k>0)于P,Q两点,点P在第一象限,如图2所示.
①四边形APBQ一定是 ;
②若点A的坐标为(4,2),则点坐标为(3,1)点P的横坐标为1,求四边形APBQ的面积;
③设点A、P的横坐标分别为m、n四边形APBQ可能是矩形吗?若可能,求m,n应满足的条件;若不可能,请说明理由.
| k |
| x |

(1)若点A的坐标为(4,2),则点B的坐标为
(2)过原点O作另一条直线l,交双曲线y=
| k |
| x |
①四边形APBQ一定是
②若点A的坐标为(4,2),则点坐标为(3,1)点P的横坐标为1,求四边形APBQ的面积;
③设点A、P的横坐标分别为m、n四边形APBQ可能是矩形吗?若可能,求m,n应满足的条件;若不可能,请说明理由.
考点:反比例函数综合题
专题:
分析:(1)点A与点B关于原点对称,所以B点坐标为(-4,-2),在第三象限当x<-4时y1>y2,在第一象限当0<x<4时y1>y2;当x满足x<-4或0<x<4时,y1>y2;当y1<2时,x的取值范围为x>4或x<0;当x>-4时,y2的取值范围为y2>-2.
(2)①由对角线互相平分的四边形是平行四边形可证明APBQ是平行四边形.
②平行四边形的对角线把它分成四个面积相等的三角形,所以只要求出△AOP的面积,再将其乘以4就可以得到APBQ的面积.
③根据对角线相等的平行四边形是矩形可知,当mn=k时OP=OA,此时APBQ是矩形.
(2)①由对角线互相平分的四边形是平行四边形可证明APBQ是平行四边形.
②平行四边形的对角线把它分成四个面积相等的三角形,所以只要求出△AOP的面积,再将其乘以4就可以得到APBQ的面积.
③根据对角线相等的平行四边形是矩形可知,当mn=k时OP=OA,此时APBQ是矩形.
解答:解:(1)∵正比例函数与反比例都关于原点成中心对称,
∴B点的坐标为B(-4,-2);
∵两个函数都经过点A(4,2),
∴双曲线的解析式为y1=
,直线的解析式为y2=
x,
∵双曲线在每一象限y随x的增大而减小,直线y随x的增大而增大,
∴当x<-4或0<x<4时,y1>y2;
当x满足x<-4或0<x<4时,y1>y2;
当y1<2时,x的取值范围为x>4或x<0;
当x>-4时,y2的取值范围为y2>-2.
故答案为:(-4,-2),x<-4或0<x<4,x>4或x<0,y2>-2.
(2)①∵正比例函数与反比例函数都关于原点成中心对称,
∴OA=OB,OP=OQ,
∴四边形APBQ一定是平行四边形.
故答案为:平行四边形;
 ②∵A点的坐标是(3,1)
②∵A点的坐标是(3,1)
∴双曲线为y=
,
∴P点坐标为(1,3),
过A作x轴的垂线CD交x轴于C,可得直角梯形OPDC,过P作PD⊥DC,垂足为D,
∴PD=3-1=2,AD=3-1=2,AC=1,OC=3,
∴S△POA=S梯形OPDC-S△OAC-S△ADP=
×(2+3)×3-
×3×1-
×2×2=4,
∴S四边形APBQ=4S△POA=16.
③四边形APBQ可能是矩形.
理由:∵当mn=k时,此时A(m,n),P(n,m),
∴OA=OP,
∵OA=OB,OP=OQ,
∴AB=PQ,
∵四边形APBQ是平行四边形,
∴四边形APBQ是矩形.
∴B点的坐标为B(-4,-2);
∵两个函数都经过点A(4,2),
∴双曲线的解析式为y1=
| 8 |
| x |
| 1 |
| 2 |
∵双曲线在每一象限y随x的增大而减小,直线y随x的增大而增大,
∴当x<-4或0<x<4时,y1>y2;
当x满足x<-4或0<x<4时,y1>y2;
当y1<2时,x的取值范围为x>4或x<0;
当x>-4时,y2的取值范围为y2>-2.
故答案为:(-4,-2),x<-4或0<x<4,x>4或x<0,y2>-2.
(2)①∵正比例函数与反比例函数都关于原点成中心对称,
∴OA=OB,OP=OQ,
∴四边形APBQ一定是平行四边形.
故答案为:平行四边形;
 ②∵A点的坐标是(3,1)
②∵A点的坐标是(3,1)∴双曲线为y=
| 3 |
| x |
∴P点坐标为(1,3),
过A作x轴的垂线CD交x轴于C,可得直角梯形OPDC,过P作PD⊥DC,垂足为D,
∴PD=3-1=2,AD=3-1=2,AC=1,OC=3,
∴S△POA=S梯形OPDC-S△OAC-S△ADP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形APBQ=4S△POA=16.
③四边形APBQ可能是矩形.
理由:∵当mn=k时,此时A(m,n),P(n,m),
∴OA=OP,
∵OA=OB,OP=OQ,
∴AB=PQ,
∵四边形APBQ是平行四边形,
∴四边形APBQ是矩形.
点评:此题属于反比例函数综合题,考查了待定系数求函数解析式的知识、反比例函数与一次函数的交点问题以及平行四边形与矩形的判定与性质.此题难度较大,综合性较强,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把方程3x+y=5改写成用y的代数式来表示x的形式是( )
| A、y=3x+5 |
| B、y=5-3x |
| C、y=3x-5 |
| D、-y=5-3x |
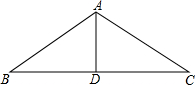 已知△ABC中,AB=17cm,BC=30cm,BC上的中线AD=8cm,请你判断△ABC的形状,并说明理由.
已知△ABC中,AB=17cm,BC=30cm,BC上的中线AD=8cm,请你判断△ABC的形状,并说明理由. 如图,在平面直角坐标系中,四边形ABCO是梯形,其中A(6,0),B(3,
如图,在平面直角坐标系中,四边形ABCO是梯形,其中A(6,0),B(3,